順像法

概要

なかなか教科書や参考書で整理されていない考え方、 順像法と逆像法。数学上級者向けの知識だとみなされることもあるが、軌跡と領域の分野では、順像法と逆像法の違いを知っておくとスッキリ理解できる問題も多い。なので、ここでは下の例題を通じて順像法の考え方を身につけよう。逆像法についてはこちらの「逆像法」の辞書を参照。

逆像法に比べると影に隠れがちだが、順像法を用いた方がスッキリ解ける問題もある。このように「okke」で検索して、順像法が活躍する演習動画をまとめて確認しよう。

例

【問】 を実数とするとき、以下の直線が通過する領域を求めよ。

【答】まずは状況を理解しよう。何を問われているかというと、 が実数の範囲で色々と動くと、こんな感じで無数のいろんな直線が生まれる。それらが通る水色の領域が、求めるものである。

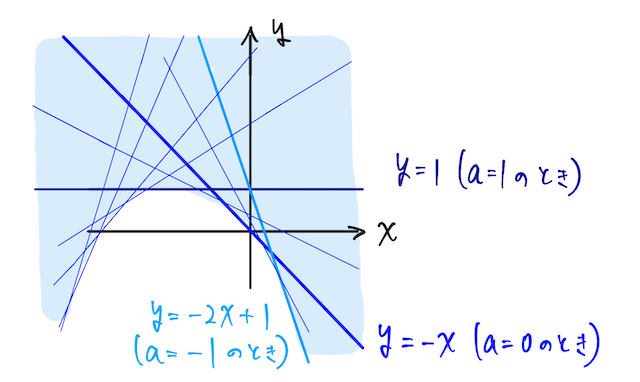
つまり、 が決まると、その直線上にある が決まって、それらは領域に含まれるというイメージ。この対応を簡単に書くとこんな感じ。

順像法では素直に、この対応に沿ってパラメータ を動かして、とりうる の値を考えていく。ただし、今回のように 変数 が動くと頭がパンクするので、片方を止めて考える（一文字固定）。

ここでは を固定して、 の取りうる値の範囲を考える。 とおくと、直線の式は

となる。ここで を の関数と見て、 を実数の範囲で動かしたときの のとりうる値の範囲（つまり値域） を考える。 次関数なので平方完成して、

となるので、 を実数の範囲で動かしたときの値域は

と求められる。固定していた を動かすと、

となり、これが求める領域となる。イメージとしてはこんな感じで、もともとある についての赤の値域を考えていたが、それを動かして、薄ピンクの領域になった感じ。

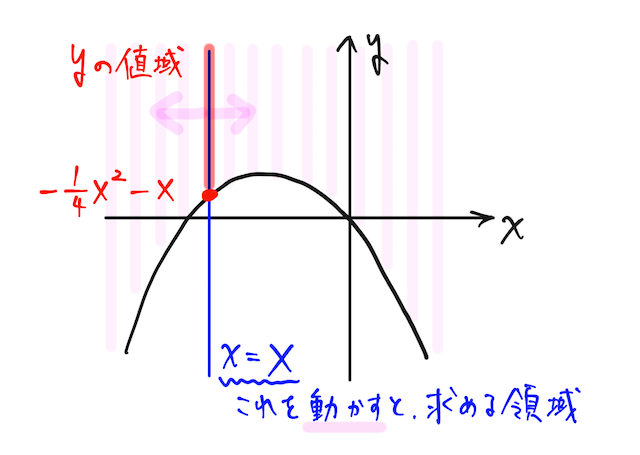
この同じ問題を逆像法で解くとどうなるか、こちらの「逆像法」の辞書で確認しよう。

補足

問題によっては逆像法のほうがラクに解ける場合も多い。二つの考え方や違いを理解して、解きやすい方を選んでいくことが大切。

東京出版（大学への数学など）では、順像法を 「ファクシミリの原理」 と読んでいたりする。ちょっとずつ読み込んでいくFAXのイメージから命名されているが、現代ではFAXは絶滅危惧種なので、すみやかな改名が待たれるところである。