概要
受験勉強で「領域」の分野を学んでいるとよく出てくる、「連立不等式によって定められたグラフの領域上を が動くときに、 の値の最大値を求めよ」みたいなパターン問題の考え方。
直接は考えにくい領域上の最大最小問題を、視覚的に考えていくのがポイントとなる。
とおいて、直線と見て、共有点をもつ条件を考える、みたいな流れ自体は頭に叩き込まれている人も多いと思うが、その意味がしっかりわかると領域の理解が深まるので、お菓子でも食べながらじっくりと考えてみよう。
例題
【問】、、 によってできる領域上を が動くとき、 のとりうる値の範囲を求めよ。
これを考えてみよう。よく参考書などに載っている解答はこんな感じ。
【解】 とおくと、これは直線 を表すので、この直線と、不等式が表す領域が共有点を持てばよい。
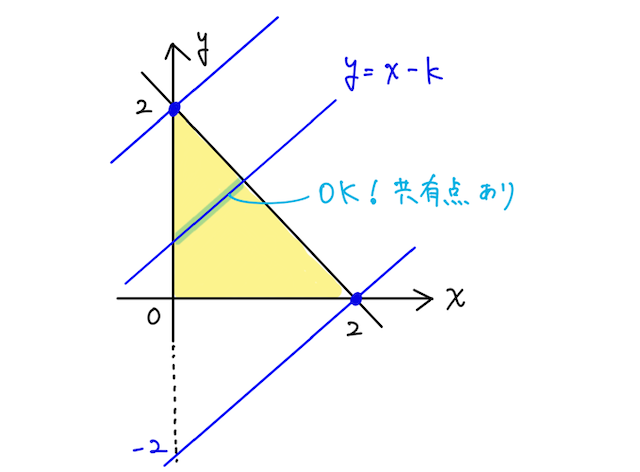
直線が を通るとき、直線の式に代入して 。
直線が を通るとき同様に 。
よって、 のとりうる値の範囲は
となるので、これが のとりうる値の範囲となる。
最初の一文が全てなんだけど、自分も含めて、「 ってなに?」「 は領域上にあるんだから直線にならなくね?」などなど、なんとも言えないモヤモヤを感じてしまう人も多い。
ここには大きく2つくらいミソが詰まっているので、とことん説明していく。
ミソ①:逆像法の考え方
まず、問題が何を聞いているかを考えてみよう。
問題の連立不等式が作るグラフ上の領域を とおく。領域 上の 点を決めると、その の値に応じて、もちろん という値が つ決まる。
ということは、素直に考えると、領域 上の全ての点に対して、 という値を計算していって、その値を全部集めたものが のとりうる値の範囲ということになる。これは納得できるはず。
でも、領域 上の点は無数にあるし、全部の点について の値を計算してかき集めてくることはできない。
じゃあどうするか。
ここで、逆像法という考えがめちゃくちゃ威力を発揮する。逆像法の詳しい解説はそっちの用語解説に譲るとして、ここではさらっと解説する。
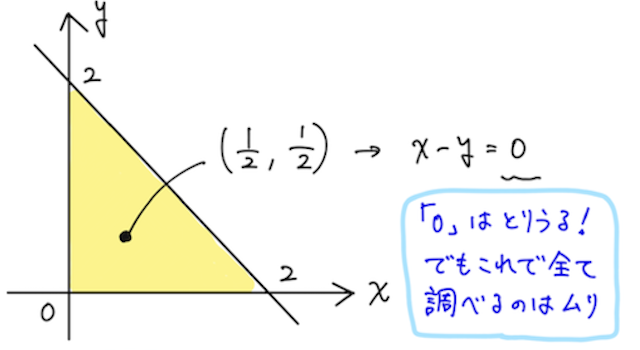
たとえば が という値をとることはあるか、を考えてみる。つまりそれは、領域を表す不等式とまとめて
を全部満たすような があるか、を考えていることに他ならない。
もしそんな があるのなら、 は という値をとり得るし、無ければとり得ないことがわかる。
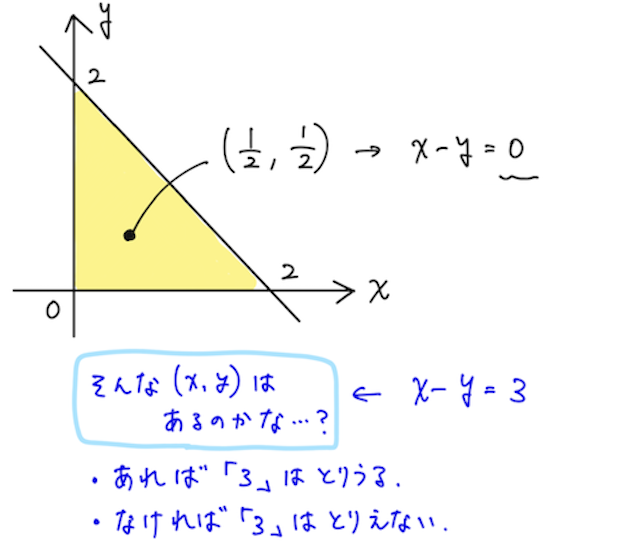
この考え方を一般化させると、 がある という値をとるかどうかは
を全部満たすような が存在するかどうかであり、ちゃんと全部満たすような が存在するような の条件(値の範囲) を求めれば、それがそのまま の、つまり のとりうる値の範囲となるのである。
これがまずは「」の正体!
ミソ②:式をグラフで捉える
ということで、逆像法のおかげで考えるべき敵はわかった。それは、
を満たすような が存在するような の条件(値の範囲)を求めること。
でも、式で眺めていても、不等式がたくさんあってややこしい。
そこで、式からグラフへの発想の転換がとても効果を発揮する。
つまり、上の つの式はぞれぞれグラフで表せるし、全ての式を満たす が存在するということは、全ての式が表すグラフに共有点が存在するということなので、以下のようにグラフ上の問題に置き換えられる。

何が嬉しいかというと、これで視覚的にラクに の条件が求められるようになったこと!
つまり、領域 も直線もすぐに書けるので、あとは共有点を持つような の条件(値の範囲)を考えればよい。
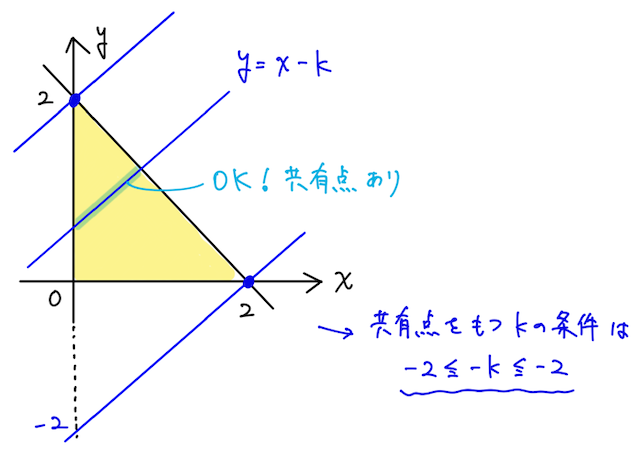
は直線の 切片のところに出てくる( 切片が )ので、直線と領域 が共有点を持つような、直線の 切片の範囲を求める。
- 直線が を通るとき、直線の 切片は
- 直線が を通るとき、直線の 切片は (傾き なので)
なので、 切片の範囲として の条件が求められて、
となるので、これで のとりうる値の範囲が求められたことになる!
補足
直線だけではなく、例えば のとりうる値の範囲やら最大値やらが問われることもあるが、考え方は全く同じ。 とおけば、今度は円を表すことになるので、円と領域が共有点を持つ条件を考えていけばOK。










