平行移動

概要

関数 のグラフを、 軸方向に 、 軸方向に だけ平行移動した関数のグラフは

となる。 は実数で、負の数でもOK。

これは、イメージとしては としてしまいそうになるし、気を抜くと出来る方でもよく間違えるので、直感に打ち勝つ理性が求められる。

理性で納得するためには、下の証明を確認しよう。考え方としては数学2で学ぶ軌跡の考え方が求められるので、まだ二次関数しか学んでいない場合には、また学習が進んだら戻ってくると、とても理解が進むはず。

動画で詳しくしっかり学びたい方は、古賀真輝さんの動画や、AKITOさんの動画がオススメ。

例

【問】 のグラフを 軸方向に 、 軸方向に だけ平行移動した放物線をグラフとする2次関数を求めよ。

【答】わざわざ平方完成して頂点を求めなくても、平行移動の式から、

と求められる。

もちろん、平方完成で新しい頂点を求めて、それを移動させてもOK。

頂点は なので、それを 軸方向に 、 軸方向に だけ移動させると、新しい頂点は となる。よって、求める二次関数は、

となる。

考え方

軌跡を使わず納得する方法

証明とは言えないが、符号を間違えないためには、次のイメージを持っておくと良い。

ある点 が のグラフ上にあるとき、代入して、

が成り立つ。

このとき、点 を 軸方向に 、 軸方向に だけ移動させると、新しい点は になる。

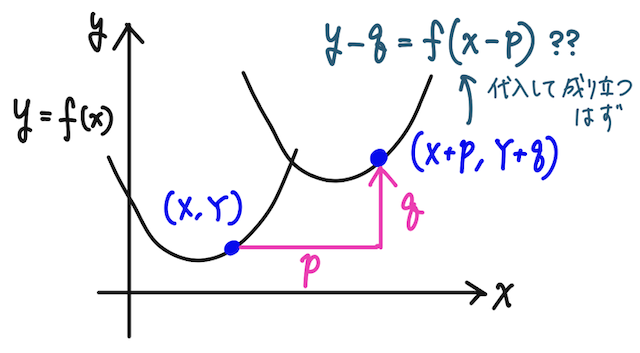
平行移動した新しいグラフ上には、この点が乗っているはずであり、関数のグラフが

であれば、新しい点の座標 を代入すると、

となり、これは確かに より成立する。

でも、もし新しい関数のグラフを

としてしまうと、点 を代入すると

となってしまって、 と別物になってしまう。なので、符号は「－」にした方が良さそうだと納得できる。

軌跡による証明

ある点 が のグラフ上にあるとき、代入して、

が成り立つ。求めるのは、 が を満たしながら動くとき、点 を 軸方向に 、 軸方向に だけ移動させた新しい点 が描く軌跡である。

そこで、この新しい点を とおくと、

これを に代入すれば（★）、

となるので、 に戻すと、求める軌跡は

となる。

（★）ここについてもっと細かく考えてみる。逆像法 の考え方を使うと、

を満たす実数 が存在するような の必要十分条件を求めれば、それが軌跡となり、それは、

だとわかる。

補足

上の証明から、 という形にならない陰関数でも成り立つことがわかる。つまり、 のグラフを、 軸方向に 、 軸方向に だけ平行移動した関数のグラフは

となる。