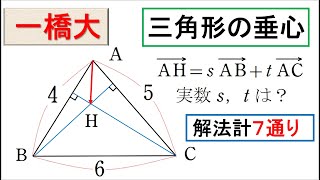
一直線上にあることの証明

＜問題＞ △ABC の辺 BC を 1:2 に内分する点を P， 辺 AC を 3:1 に内分する点を Q，辺 AB を 6:1 に外分する点を R とするとき，3 点 P，Q，R が一直線上にあることを示せ. 3つの解法を紹介します。複数のアプローチを考えることは、理解を深めることにつながります。 ＜この動画について＞ メネラウスマニアが好きそうな問題が続いておりますが， ベクトル初心者の人は解法1の単純作業感に着目です． すぐに役立つものはすぐに役立たなくなる． シリーズ「ベクトルに捧げる，2020夏。」も3日目/33日間 です． 平日もなんとかUPできました！果たして完走できるのか!? ＜目次＞ 00:00 問題説明 00:24 解1 一方が他方の実数倍 02:46 解2 係数の和が1 03:56 解3 メネラウスの定理 04:31 まとめ ＜キーワード＞ #一直線上 #共線条件 #係数和が1 #始点を揃える ＜はやくち解説とは＞ かったるい説明に嫌気がさしたときに見る動画。早口×早送りで解説しました。雰囲気を掴んでもらえたらいいと思っています。 ＜使用機材＞ カメラ：iPhone 11 Pro タブレット：iPad Pro 12.9インチ アプリ：Good Notes 5 編集ソフト：Final Cut Pro