単振動

概要

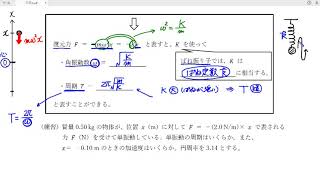
等速円運動する物体を真横から見たときの、一直線上の往復運動を、単振動という。ばねにつけたおもりの往復運動と同じような運動になるので、単振動というネーミングは理解できると思う。

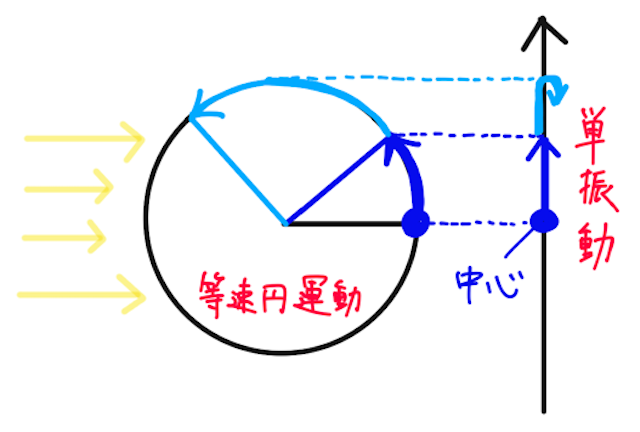
単振動について、振動の中心から振動の端までの長さ を振幅（端から端までにしないように！）、1回の振動に要する時間 を 周期 という。実は下で見るように、単振動の変位は正弦曲線を描くので、物理量の名前も波動と共通している。

単振動は、運動方程式を解くのが難しい（※）ので、等速円運動のときと同様、特別な場合として、運動（変位・速度・加速度）の記述を理解する必要がある。

（※ 微分方程式という強そうなものを解くことになる、気になる方はこの単振動の一般解の辞書を参照）

一般の結論としては、もとの等速円運動の半径を （これが単振動での振幅になる）、角速度を （これを単振動の分野では角振動数と呼ぶ）とし、時刻 に、時刻 に下の通り角度 の位置にあり、ここから正の角度の向きに回転するとする（このような を初期位相という）。振動の中心を とすると、

• 単振動の変位

• 単振動の速度

• 単振動の加速度

とそれぞれを時刻 で表すことができる。逆にいうと、このような表され方をするような運動は全て単振動である。

単振動の変位・速度・加速度の式について、まずは、等速円運動を用いた教科書的な証明を載せてみるが、微分で理解するとラクなので、数学3まで学んだ方のためにその方法も後で紹介する。ラクするためにも是非理解しておこう。

参考になる動画をあげておくので、文章じゃちょっとわからん！という方はこちらを見てみよう。

• 教科書的な証明：ちょこっと物理さん、Try ITさん（計3つ）、ただよび・飯泉先生
• 微分での証明：CSS高校物理さん、受験メモ山本さん

単振動の変位

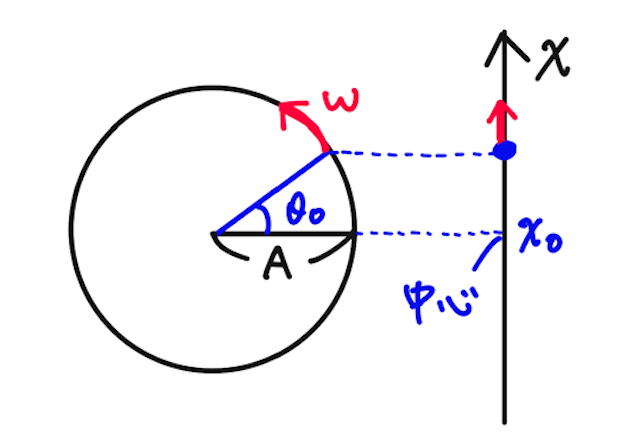
等速円運動の半径を 、角速度を （これを単振動の分野では角振動数と呼ぶ）とし、時刻 に、時刻 に下の通り角度 から正の角度の向きに回転するとする。また、円の中心の高さを とする。このとき、等速円運動を横から見たときの変位は、下の図の黄色の直角三角形に注目すると、

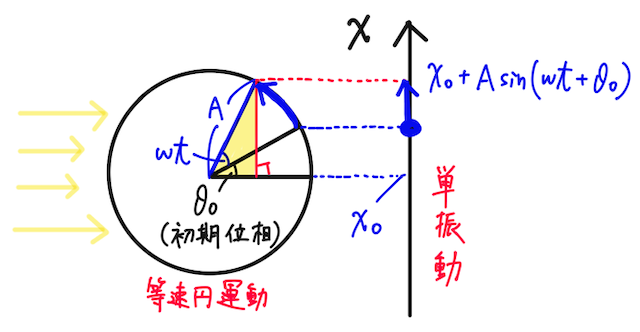
となることがわかる。これがこの単振動の変位を時刻 で表した式。 は振動中心と呼ばれる。

単振動の速度

単振動の速度も同様に、等速円運動の速度ベクトルを横から見たときの様子を調べればよい。下の図の黄色の直角三角形に注目すると、

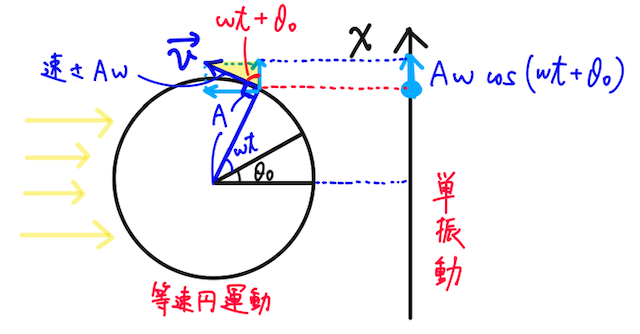
斜辺の長さが速さ、つまり なので、横から見たときのベクトルは、上を正として

と表される。これがこの単振動の速度を時刻 で表した式。

単振動の加速度

単振動の加速度も同様に、等速円運動の加速度ベクトルを横から見たときの様子を調べればよい。等速円運動の加速度は中心方向を向き、下の図の黄色の直角三角形に注目すると、

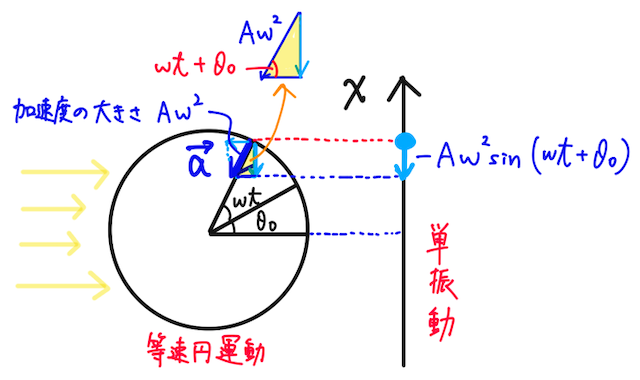
斜辺の長さが加速度の大きさ、つまり なので、横から見たときのベクトルは、上を正として

と表される。これがこの単振動の加速度を時刻 で表した式。

単振動の運動方程式

単振動では、上で見た通り加速度が生じており、

このように、加速度は振動中心からの変位（）の向きとは逆向きに生じる。

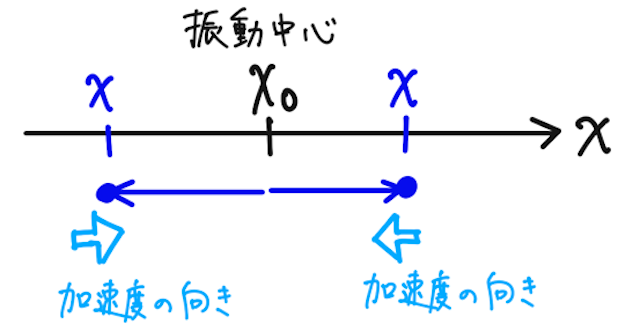
ということは、運動方程式より、物体には、振動中心に向かう方向に何かしらの力を受けていることがわかる。その力のことを復元力という。つまり単振動を引き起こすような力のこと。

質量 の物体が単振動しているとすると、運動方程式より

式からも、復元力が振動中心からの変位の大きさ（）に比例し、向きは逆向きであることがわかる。

逆にいうと、運動方程式を考えて、変形をして、加速度と変位の間に以下の関係が成り立つ運動は、振動中心 、角振動数 の単振動であることを意味する。

例えば簡単な例として、水平のばね振り子を考えよう。

【例】ばね定数 のばねの一端を壁に固定し、自然の長さから だけ引っ張り、質量 の小球をつけて手を離した。自然長を原点とし、下のように正の向きを取るとき、単振動の周期・位置の式・速度の式・加速度の式を求めよ。

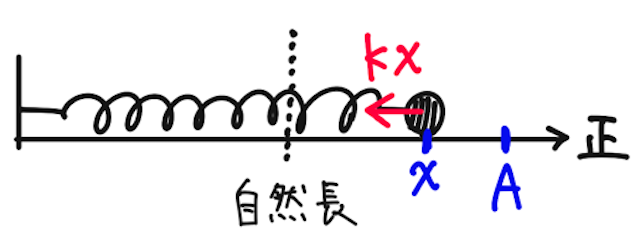
【答】位置 での運動方程式は、

なので、振動中心が の単振動をしている。

また、角振動数は、

より、

であることが分かる。

よって、周期については、

と分かる。また、単振動の変位については、あと振幅と初期位相が分かれば、上で示した形で表すことができる。 これらについては、今回の初期条件（一番変位が大きいところで離していること）を考えると、それぞれ と であることが分かるので、あとはそれぞれ上で示した形に代入すれば、

と求められる（90°関係の辞書を参照）。同様にして、

と求められる。

（発展）微分で理解

単振動の変位さえ求めてしまえば、上で示した単振動の速度・加速度は微分ですぐに求めることができる。変位の式を

とすると、時間で微分すれば速度が求められて、

さらにこれを時間で微分すれば加速度が求められて、

とすぐに上の式が導ける。（三角関数の導関数の公式 / 合成関数の微分公式 の知識が必要）

さらに、変位の式と加速度の式を見比べると、加速度と変位の関係式

が必ず成り立つことがわかる。

上のセクションの例題で求めた速度・加速度の式も、是非微分で求めてみよう。

補足

実践上は、教科書的な定義を使って「ああ、これはこの等速円運動を横から見ているから単振動だな」みたいに優雅に判断することはほぼやらない。問題を解くときには、上の運動方程式のセクションで学んだ通り、とりあえず力を見つけて物体の運動方程式を書いて、加速度について変形して、もし

の形に持っていけたら、そこで初めて 「あ、単振動なんだ、振動中心は だな、角振動数 はこう表されるな、あとは初期条件（最初の状態）考えたら、変位・速度の式はこれで表されるな」 という流れで考えていくことが多い。

冒頭でも少し触れた通り、こちらの単振動の一般解の辞書を参照。これを知っておくと、運動方程式を立てればなんとかなるという最終境地に達することができるので、単振動の分野について覚えるものや怖いものがなくなる。