固有周波数

概要

充電したコンデンサーにコイルをつなぎ、放電させると、一定の周期で向きが変わる電流（振動電流）が流れる。この現象のことを電気振動という。

電気振動における振動回路の周波数 は、コイルの自己インダクタンスを 、コンデンサーの電気容量を とおくと、

で表せる。（振動電流の周波数ももちろんこれになる）

この周波数のことを固有周波数という。

詳細

電気振動のイメージとしては、こんな感じ。

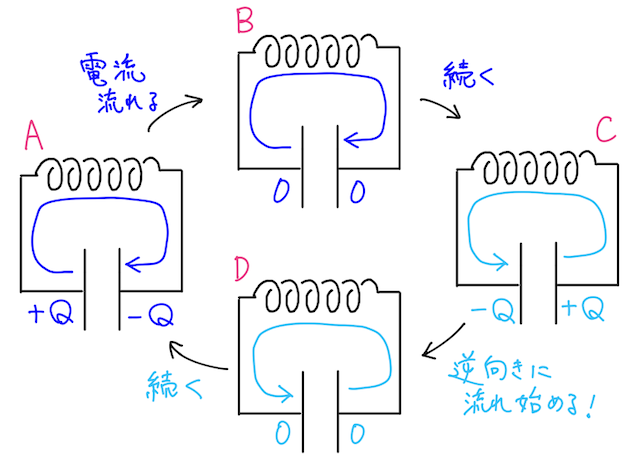
充電された状態（）から、放電によって電流がコイルに流れていくと、いずれコンデンサーに蓄えられた電荷が になる（）。しかし、コイルは電流の変化を妨げようとするので、コンデンサーの電荷が になっても電流はすぐには にならず、コンデンサーの電荷はそのまま逆符号で溜まり始める（）。コンデンサーの充電が完了すると、また放電により逆向きの電流が流れ始め（）、この流れを繰り返していく感じ。

では、固有周波数の式を導出しよう。

回路を見ると、コンデンサーとコイルが直列につながっているだけなので、常に、この つを流れる電流は等しく、それぞれの電圧の大きさも等しい。

よって、コンデンサーとコイルのそれぞれに対して、電流の最大値と 電圧の最大値は同じになるので、それぞれの リアクタンスの値が一致する。（リアクタンスについて知識が怪しい人は、リンクを飛んで確認！）

よって、電気振動での振動電流の角周波数を 、コイルの自己インダクタンスを 、コンデンサーの電気容量を とおくと、

が成り立つので、電気振動を行う回路の角周波数 は

と求めることができる。このとき、回路の周波数 は

と表せる。これを電気振動を行う回路の固有周波数という（もちろん振動電流の周波数もこれになる）。導出できるようにしておこう！

※ 上の周波数と角周波数の関係式は、周期 を介して考えるとわかりやすい。つまり、（これは波動で頻出の式！）と の関係式が成り立つので、これから を消去すれば、周波数と角周波数の関係式

が得られる。

補足

似た用語に 「共振周波数」 というものがあり、式も同じだが、出てくる場面が違う。

共振周波数というのは、 直列回路において、特定の周波数で大きな電流が流れる現象（共振）が起こるときの周波数のこと。区別しておこう！