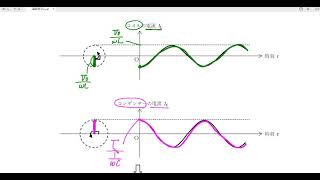
インピーダンス

概要

※まず、リアクタンスって何？美味しいの？という方は先にリアクタンスを学びましょう。

リアクタンスでは、1つの素子について電流の流れにくさ、抵抗のようなものを考えたが、回路全体についても考えてみよう。

つまり、回路全体を流れる交流電流 と、回路全体に加わる交流電圧 の間の関係を調べる。リアクタンスのときと同様、やっぱり回路全体を考えても電流と電圧に位相が違ってくるので、合成抵抗のときのように単純に割り算してもあまり面白くない。

そこで、リアクタンスのときと同じように、電圧の最大値 を電流の最大値 で割った値を考える。こうすると時間によらない値が出てきて嬉しい。このようにして出てきた、回路全体の交流に対する抵抗のようなものをインピーダンスという。ダンスが入ってて楽しげな名前だが、電磁気の最後の方に出てきてちんぷんかんぷんで終わりがちなテーマなので、しっかりと流れを理解しよう。

これは 実効値 でも表すことができて、実効値は最大値を で割ったものであるので、

でも求めることができる。単位は、定義からわかる通り、抵抗と同じオーム を用いる。

では、代表的な交流回路である、RLC直列回路、RLC並列回路でインピーダンスを求めてみよう。それぞれの素子の間で何が共通しているのか（電流なのか、電圧なのか）を理解して式を立てていくのがとても大事。

数式で考えたほうが頭がすっきりとすると思うので、ここでは数式で処理していくが、教科書に載っているようなベクトルを用いた図で理解したいという方は、この受験メモ山本さんの動画を見てみよう！数式でもベクトルでも解説されていて、とてもわかりやすい。

RLC直列回路

下の図のように、抵抗値 の抵抗 、自己インダクタンス のコイル 、電気容量 のコンデンサー を交流電源に直列につないだ回路を考える。このような回路は、これらの名前をそのまま続けて、RLC直列回路と呼ばれる。

各素子に流れる電流は共通しており、その電流を

とおく。このときに、交流電源の交流電圧 がどのように表されるかを考えよう。

そのために、抵抗やリアクタンス、位相のずれなどを考えつつ、各素子での電圧を考えていこう。

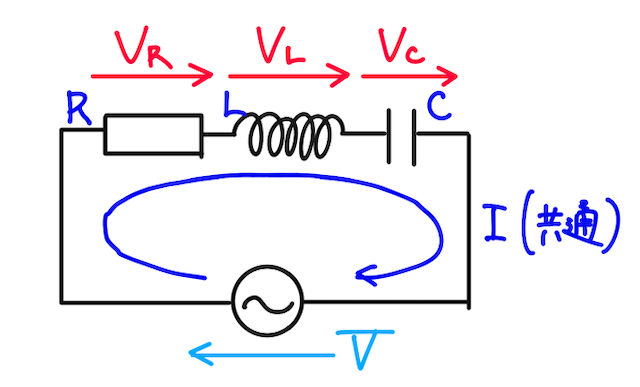
抵抗での電圧

オームの法則より、

と求まる。

コイルの電圧

リアクタンスの辞書で学んだ通り、コイルのリアクタンス と位相のずれで考えでみよう。

コイルでは、電圧の最大値 と電流の最大値 の間には、

が成り立ち、さらにコイルを流れる交流電圧の位相は電流の位相に比べて 進むので、電圧 は、

と表される。

コンデンサーの電圧

コイルと同様、リアクタンスの辞書で学んだ通り、コンデンサーのリアクタンス と位相のずれで考えでみよう。

コンデンサーでは、電圧の最大値 と電流の最大値 の間には、

が成り立ち、さらにコンデンサーを流れる交流電圧の位相は電流の位相に比べて 遅れるので、電圧 は、

と表される。

キルヒホッフの第二法則より、交流電源の交流電圧 はこれらを足し合わせればよく、

となる。インピーダンスを求めるために、右辺の最大値が知りたいので、 に変形しつつ三角関数の合成でまとめていく。

ただし、 は

を満たす角度。

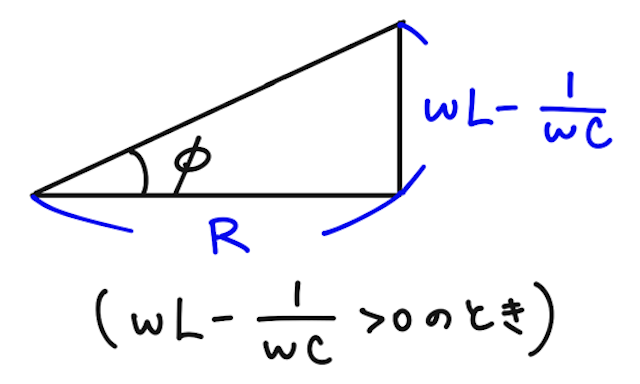
よって、交流電源の交流電圧 の最大値 は、

となるので、インピーダンスは、定義から電圧の最大値 を電流の最大値 で割った値なので、

と求まる。

おまけで、共振周波数についても押さえておこう。

同じ最大値 を持つ交流電圧をかけても、その周波数 を変えることで、角周波数 が変わる。そうすると、上で求めたインピーダンスの値が変わるので、RLC直列回路を流れる交流電流の最大値 を変えることができる。

では、周波数 をどのような値にすれば、流せる電流が最大になるだろうか。

を考えると、インピーダンスが最小になるときに、電流の最大値は最も大きくなることがわかり、上で求めたインピーダンスの式から、それはつまり

が成り立つとき、つまり

のときである。このときの周波数 は

となる。これを共振周波数といい、このとき非常に大きな電流が回路に流れることになる。テレビやラジオの電磁波の受信回路に用いられる大事な性質である。

RLC並列回路

下の図のように、抵抗値 の抵抗 、自己インダクタンス のコイル 、電気容量 のコンデンサー を、今度は交流電源に並列につないだ回路を考える。このような回路は、これらの名前をそのまま続けて、RLC並列回路と呼ばれる。

各素子に加わる電圧は共通しており、その電圧を

とおく。このときに、回路を流れる交流電流 がどのように表されるかを考えよう。

そのために、抵抗やリアクタンス、位相のずれなどを考えつつ、各素子に流れる電流を考えていこう。

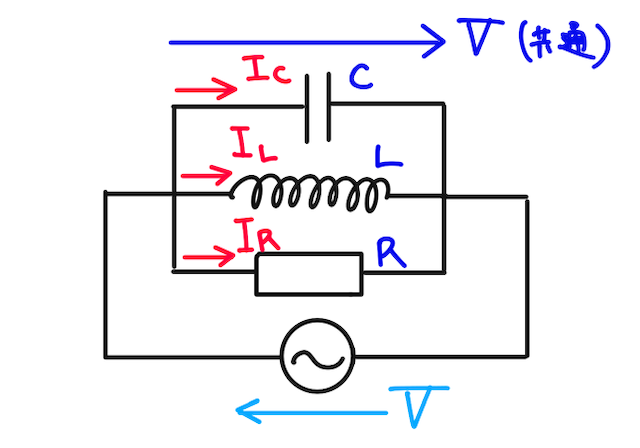
抵抗を流れる電流

オームの法則より、

と求まる。

コイルの電流

リアクタンスの辞書で学んだ通り、コイルのリアクタンス と位相のずれで考えでみよう。

コイルでは、電圧の最大値 と電流の最大値 の間には、

が成り立ち、さらにコイルを流れる交流電流の位相は電圧の位相に比べて 遅れるので、電圧 は、

と表される。

コンデンサーの電流

コイルと同様、リアクタンスの辞書で学んだ通り、コンデンサーのリアクタンス と位相のずれで考えでみよう。

コンデンサーでは、電圧の最大値 と電流の最大値 の間には、

が成り立ち、さらにコンデンサーを流れる交流電流の位相は電圧の位相に比べて 進むので、電圧 は、

と表される。

キルヒホッフの第一法則より、回路全体を流れる電流 はこれらを足し合わせればよく、

となる。インピーダンスを求めるために、右辺の最大値が知りたいので、 に変形しつつ三角関数の合成でまとめていく。

ただし、 は

を満たす角度。

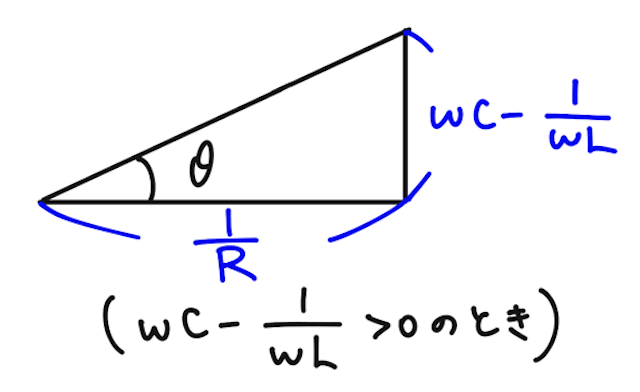
よって、回路全体の電流 の最大値 は、

となるので、インピーダンスは、定義から電圧の最大値 を電流の最大値 で割った値なので、

と求まる。