リアクタンス

概要

交流回路では、電流の向きや大きさが常に変化している（ や がくっついてくる）。交流回路に、抵抗ではなく、コイルやコンデンサーを接続したときに、電流の流れにくさをどうやって表すかを考えよう。

抵抗の場合は、オームの法則から、

で求めることができたし、交流回路でもこれで求められる。

しかし、コイルやコンデンサーの場合には、下で見るように電圧と電流の位相（ や の中身の角度）が異なってくるので、単純に割り算をしてもあまり役に立たない。

そこで、少し工夫をして、電圧の最大値 を電流の最大値 で割った値を考える。こうすると時間によらない値が出てきて嬉しい。このようにして出てきた、コイルやコンデンサーの交流に対する抵抗のようなものをリアクタンスという。

これは 実効値 でも表すことができて、実効値は最大値を で割ったものであるので、

でも求めることができる。単位は、定義からわかる通り、抵抗と同じオーム を用いる。

下で詳細を学ぶが、結論としては、

• コイルのリアクタンス（誘導リアクタンス）

• コンデンサーのリアクタンス（容量リアクタンス）

となる。

親戚にインピーダンスという楽しげな概念もあるが、違いについては、インピーダンスの辞書を参照。

動画でしっかりと学びたい方は、受験メモ山本さんの動画がオススメ。また、以下見ていくように、位相のずれなどを頭に入れるのがとてもややこしく「いちいち証明してられない、覚える裏技はないのか！」という方にはまことさんの動画がオススメ。

コイルのリアクタンス

自己インダクタンス のコイルと交流電源が接続された回路を考える。コイルに加わる電圧（電位差） が

で表されるとする。

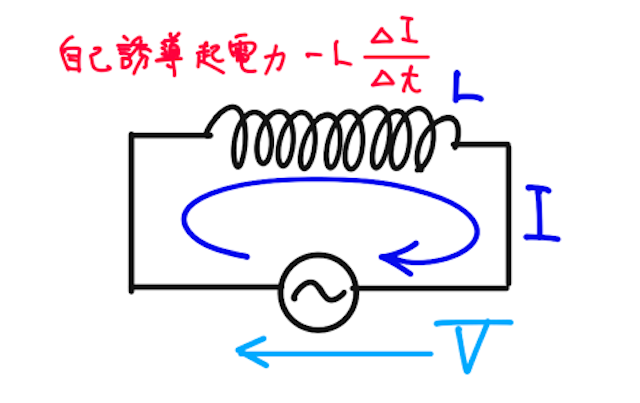
この回路に流れる交流電流を とおくと、キルヒホッフの第二法則より、

となる（自己誘導起電力はこちらから）。

時間を短くしていき、交流電流の式を求めると、

となる。（三角関数の積分を利用した）

よって、コイルのリアクタンスは、定義から電圧の最大値を電流の最大値で割ればよく

と求められる。これを誘導リアクタンスとも呼ぶ。

また、コイルを流れる交流電流と交流電圧の位相のずれも押さえておこう。交流電流の式を変形すると、

となる（90°関係の辞書や、加法定理と関連づけて理解できる）。よって、コイルに加わる電流の位相は、電圧の位相よりも だけ遅れている。式で確認するクセをつけておくと、どっちがどっちより進んでいるのか忘れない。

ちなみに、コイルでの消費電力 は、

と求められる（2倍角の公式を用いた）。よって、時間平均するとコイルでの消費電力は0になる。

コンデンサーのリアクタンス

電気容量 のコンデンサーと交流電源が接続された回路を考える。コイルに加わる電圧（電位差） が

で表されるとする。コンデンサーに電荷 が蓄えられているとする（ややこしいので、電流の向きを考えて、蓄えられていく方を にしよう）。

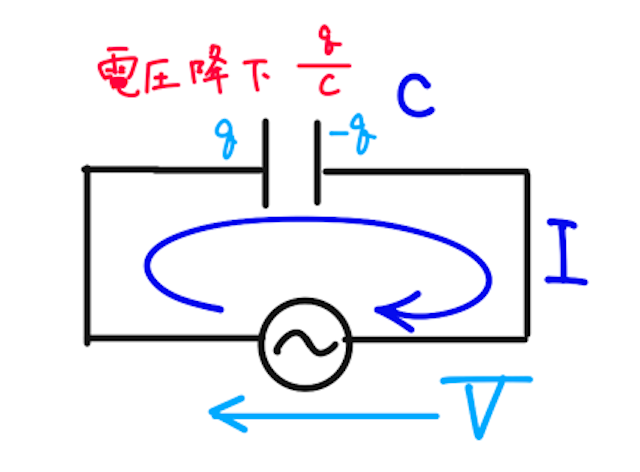
この回路に流れる交流電流を とおくと、キルヒホッフの第二法則より、

と立式できる。（電気容量の定義より、コンデンサーでの電圧降下は ）

ここで、電流の定義より、

時間を短くしていき、交流電流の式を求めると、

となる。（三角関数の導関数を利用した）

よって、コンデンサーのリアクタンスは、定義から電圧の最大値を電流の最大値で割ればよく

と求められる。これを容量リアクタンスとも呼ぶ。

また、コンデンサーを流れる交流電流と交流電圧の位相のずれも押さえておこう。交流電流の式を変形すると、

となる（90°関係の辞書や、加法定理と関連づけて理解できる）。よって、コンデンサーに加わる電流の位相は、電圧の位相よりも だけ進んでいる。式で確認するクセをつけておくと、どっちがどっちより進んでいるのか忘れない。

ちなみに、コンデンサーでの消費電力 は、

と求められる（2倍角の公式を用いた）。よって、時間平均するとコンデンサーでの消費電力は0になる。

補足

似たような用語に、インピーダンスという楽しげなものがあるが、これはコイルや抵抗やコンデンサーやらがつながった回路全体を考えたときの電流の流れにくさを表すもの。それに対して、このリアクタンスは、個々のコイルやコンデンサーについての電流の流れにくさを表すもの。

いわば、インピーダンスは合成抵抗のようなイメージ。（位相のずれがあるから、合成抵抗よりはややこしい）

上でも紹介した通り、動画で学びたい方は、受験メモ山本さんの動画を見てみよう。また、位相のずれなどがややこしいので、「いちいち証明してられない、覚える裏技はないのか！」という方にはまことさんの動画がオススメ。「CIVIL」という便利な技が学べる。