三平方の定理
概要
直角三角形の三辺の長さについて、次の関係式が成り立つことを三平方の定理という。
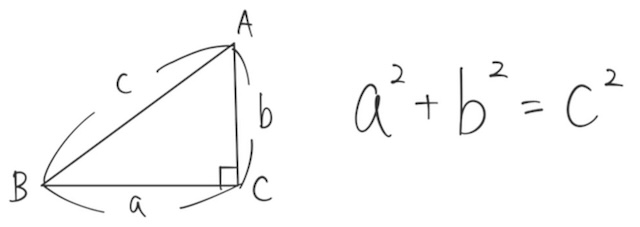
「ピタゴラスの定理」とも呼ばれるが、高校数学では「三平方の定理」と書かれていることが多い。画数は「三平方の定理」の方が
証明
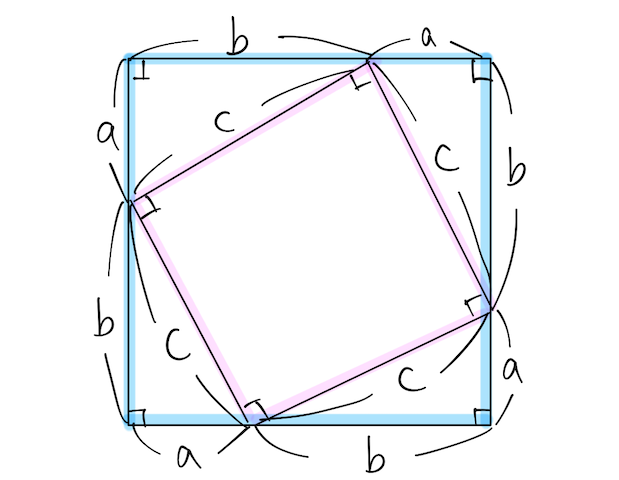
上の図で、大きい正方形(水色)の面積を
①一辺の長さの
②小さい正方形(ピンク)+
これらが等しいので、
が示される。
補足
逆も成り立つ。つまり、三辺の間に
の関係が成り立つ三角形は、
また、
この用語を含むファイル
関連動画
関連用語
直角三角形の三辺の長さについて、次の関係式が成り立つことを三平方の定理という。
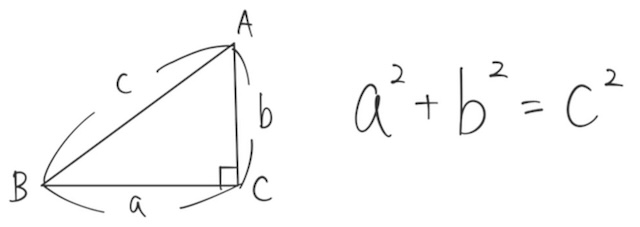
「ピタゴラスの定理」とも呼ばれるが、高校数学では「三平方の定理」と書かれていることが多い。画数は「三平方の定理」の方が

上の図で、大きい正方形(水色)の面積を
①一辺の長さの
②小さい正方形(ピンク)+
これらが等しいので、
が示される。
逆も成り立つ。つまり、三辺の間に
の関係が成り立つ三角形は、
また、
この用語を含むファイル
関連動画
関連用語