概要
これまで、平面上の点の位置を (直交座標)で表してきたが、それを、 原点からの距離 と、 軸の正の向きからの角度 で測った座標のことを、 極座標という。
これを用いて、複素数平面上の複素数 を極座標表示したものを、 極形式という。
直交座標での表示 と極座標での表示の関係式は、下の図からわかる通り、
であり、これを用いると、この複素数の極形式は以下の形になる。
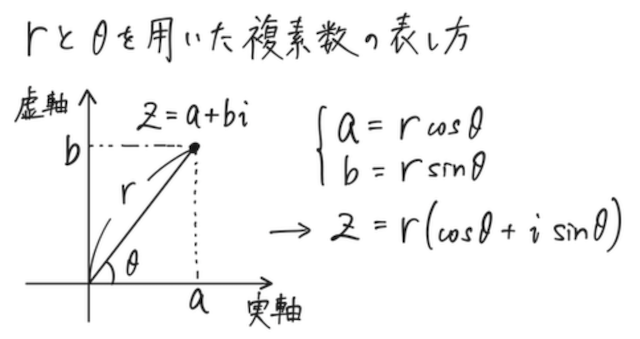
と には名前がついていて、 を複素数 の絶対値、 を複素数 の偏角という。
例
の極形式は、
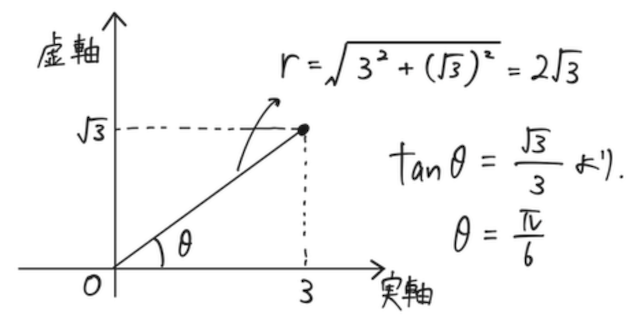
より、
このように、極形式に変形するときは、 と を決める必要があるが、 グラフで考えるとわかりやすい。
補足
極形式では、 が の角度とまぎらわしいので、 を前に出すことが多い(直交座標での表示()の時は、基本的に はうしろに来る)。
なぜ でくくったかについては、 の部分と の部分を分けると、複素数の掛け算や割り算をスッキリ考えることができて、楽しいことが起きるからである(例えば「ド・モアブルの定理」が使える)。これが極形式の醍醐味である。
また、(つまり複素数平面での原点)を極形式で表すと、 は任意となる。( の情報だけで原点が表されることになる)



