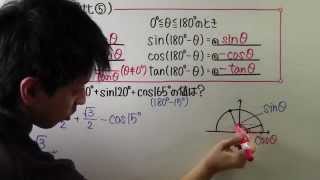tan

概要

「たんじぇんと」と読む。ひらがなにすると弱くなる数学用語ランキング上位。

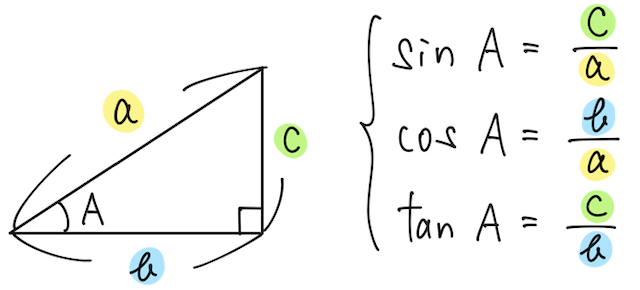
覚え方としては、こんな感じで、それぞれの頭文字「s, c, t」を筆記体で書いて、三角形の辺をなぞっていき、分母→分子の順に並べるものが有名。

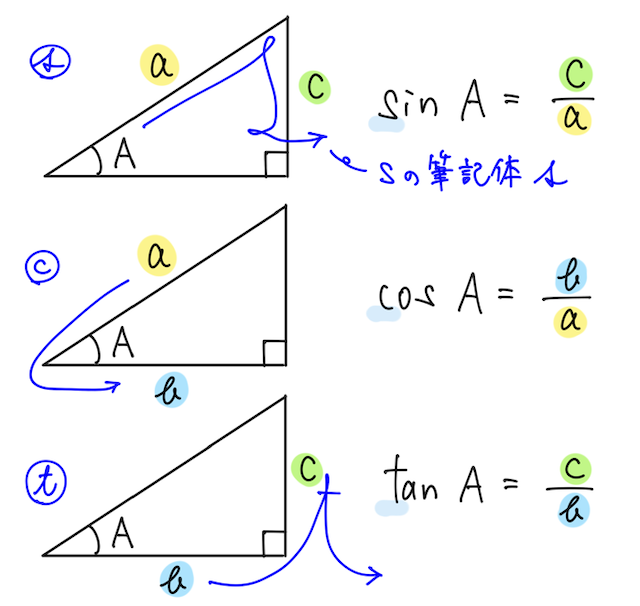
とりあえず、これは定義なので覚える必要あり。 覚え方はなんでもいいので、確実に覚えよう！

背景

なぜこんなものを考えるのか、というところを少し学んでみよう。

実はどんな直角三角形であっても、その辺の「比」は、直角でない つの角の大きさによって完全に決まる。（直角でない つの角が等しいと、内角が全て等しくなり相似になるため）

そこで、その辺の比をこのように分数で表すことにする。

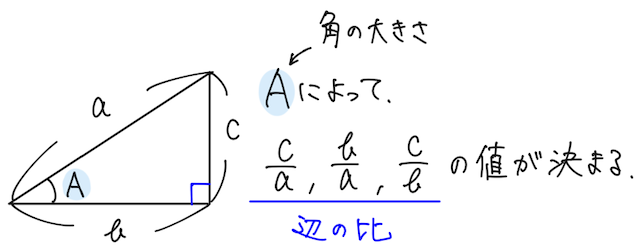
これらの値は、角の大きさ だけによって つに決まるため、それぞれの値を 、、 と定義した、という流れ。

ちなみに、

• の値を のサイン（正弦）
• の値を のコサイン（余弦）
• の値を のタンジェント（正接）

と呼ぶ。

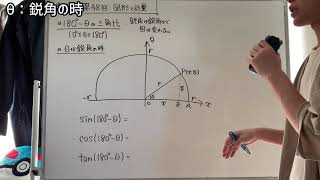
三角比の拡張

この直角三角形の定義では 〜 でしか三角比を定義できないので、より広い定義を考える。

それが単位円（半径が の円）を用いた考え方で、 は動径の傾きとして定義される。（動径は、単位円の中心から、ある角度の方向へ伸びる半直線のこと）

つまり、 軸正の向きから測った角度 （時計回りを正、反時計回りを負）が決まると、単位円上の動径も決まって、その傾きを の値とする。

同様に、 は単位円上の 座標、 は単位円上の 座標として定義される。

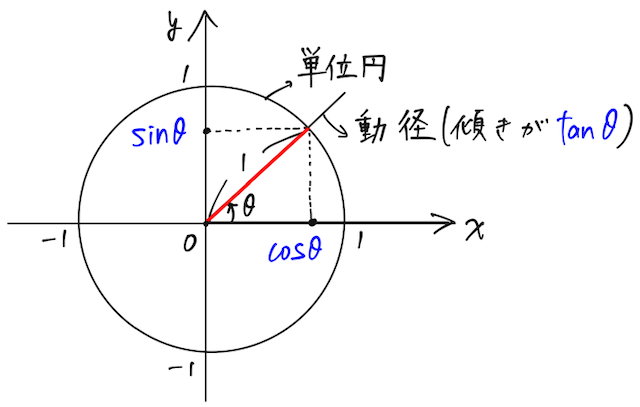
数学Ⅰの三角比では、 〜 の範囲で考えるが、数学Ⅱの三角関数になると、もっとグルグル回る。考え方は基本的に上と同じなので、余裕があれば先取りしてしまおう。