二次曲線の極方程式
概要
という形の極方程式は、
この
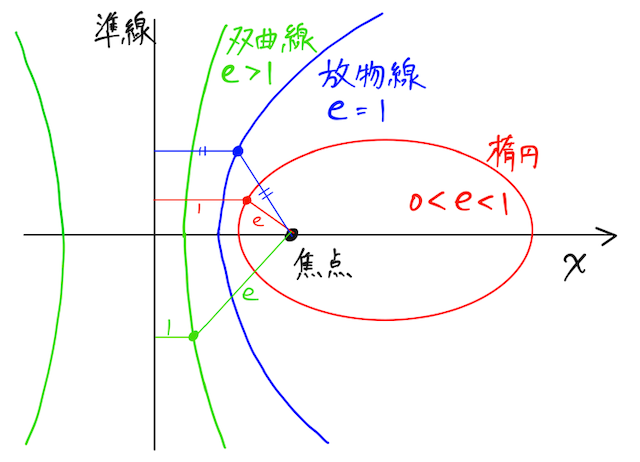
:楕円 :放物線 :双曲線
となる。
説明
まず、ある定点
:楕円 :放物線 :双曲線
を表す。この
ここで、今回考えている極方程式
この式をグラフ上で捉えると、
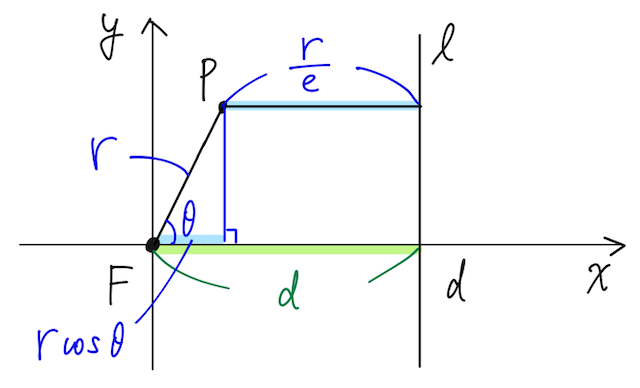
となるので、極方程式
(ここでは点
よって、極方程式
補足
極方程式
についても、
と変形できるので、
また、
一方で、極方程式では負の
興味がある方は、ぶおとこばってんのこの動画で深掘りしてみよう。
関連動画
という形の極方程式は、
この
となる。
まず、ある定点
を表す。この

ここで、今回考えている極方程式
この式をグラフ上で捉えると、

となるので、極方程式
(ここでは点
よって、極方程式
極方程式
についても、
と変形できるので、
また、
一方で、極方程式では負の
興味がある方は、ぶおとこばってんのこの動画で深掘りしてみよう。
関連動画