浮動小数点数

概要

コンピュータは、CPUが処理可能なデータのビット数や、CPUとメモリの間で送信可能なデータのビット数に制限がある。

そこで、小数点を含む数をコンピュータで扱うとき、小数点以下どこまでを表現するかが問題となる。

「小数第何位までしか読み取りません」と固定してしまうと、コンピュータで取り扱える値の精度が落ちてしまうので、値の表現の中に小数点の位置の情報を組み込んでしまって、小数点の位置を固定せずに済むような工夫がなされている。その表現方法で表された数を浮動小数点数という。

この問題で、浮動小数点数の仕組みをしっかりと身につけよう。一度理解できてしまえば困ることはないし、工夫のポイントがわかればかなり面白いことをやっていることがわかるので、じっくり考えてみよう！

詳細

例を通じて考えた方がわかりやすいと思うので、例えば という 進数を、 ビットの 進数の浮動小数点数（符号部 ビット、指数部 ビット、仮数部 ビット）で表してみよう。

※ 細かい用語は途中で説明するのでとりあえず進めてみよう！

まず、表現したい数を、整数部分が ではない 桁になるようにズラして調整する。

例えば、今回の だと

だし、他の適当な例だと

のようなイメージ。

次に、値の符号、小数点以下の値、 の何乗か、の情報を、以下のように、まとめて合計 ビットの中に格納する。

※ ）図のように、浮動小数点数の表示で、冒頭の正か負かを表す部分を符号部、 の何乗かを表す部分を指数部、小数点以下の部分を仮数部という。

※ ） 進数の場合、上で変形した値の整数部分は必ず となることから、小数点以下のみ格納すれば元の数を復元できるので、図のピンクの箇所の通り、仮数部に格納するのは、小数点以下の部分の値のみでOK！

※ ）指数部については、問題文の指示通り、元々の指数の に を足して 、これを 進数にした を指数部に格納する点に注意。

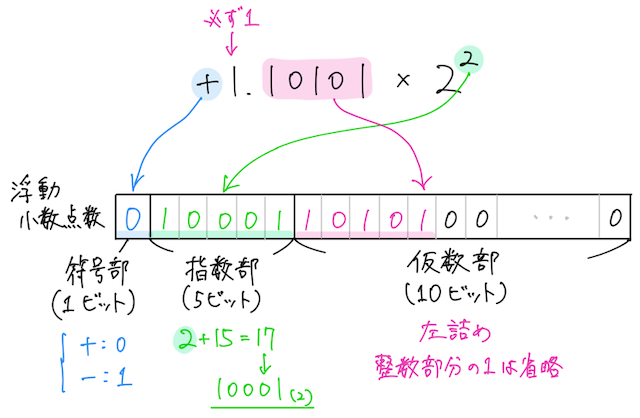
→ 一定の値を足したものを指数部に格納する理由は、負の指数を持つ数も表せるようにするため。この工夫により、例えば みたいなめちゃくちゃ小さい数まで浮動小数点数で表現できることになる！

よって、求める ビットの浮動小数点数は、左から読んでいって

となる。

この表現方法により、この つの情報が揃えば元の値が分かるし、この表し方をすれば、元の小数点の位置に関わらず、ある程度の精度で元の数を表現できているというのが重要なポイント！

補足

今回の、符号部 ビット、指数部 ビット、仮数部 ビットで表す方法を半精度浮動小数点数といい、他にも、

• 合計 ビット使う単精度（符号部 ビット、指数部 ビット、仮数部 ビット）
• 合計 ビット使う倍精度（符号部 ビット、指数部 ビット、仮数部 ビット）

があり、実際には倍精度で表現されるコンピュータが多い。

また、例えば倍精度で ビット使ったとしても、値が大きすぎてビット数が足りず表せなかったり（オーバーフロー）、値が小さすぎて表せなかったり（アンダーフロー）して、コンピュータで正確な値を表せない場合が出てくる。その場合には、切り捨てや切り上げ、四捨五入などの 「丸め」 という操作が行われることになり、それによって発生してしまう、実際の値と浮動小数点数で表される値との誤差のことを丸め誤差という。

もっと補足

半精度浮動小数点数（ ビット）では、指数部が の場合は などを、 の場合は無限大などを表したりと、特殊な使われ方をするため、基本的に指数部は 〜 を用いる。

このもとで、半精度浮動小数点数で表せる値の範囲を考えてみよう。（ここではとりあえずプラスの値を考えるが、符号部を変えればマイナスの値も表せる点に注意！）

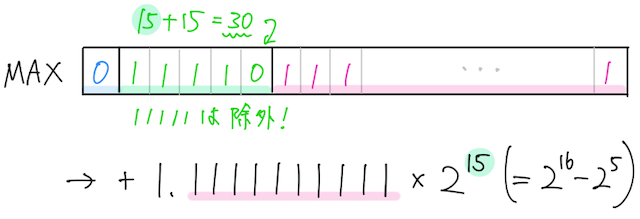
最大の値（無限大などを除く）は、指数部が のときであり、 ビットの 進数の浮動小数点数が

となるときである。

つまり大きい数については、 まで正確に表すことができる。整理すると、

となる。

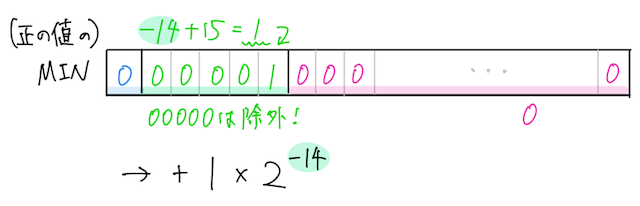
一方で、最小の値は、指数部が のときであり、 ビットの 進数の浮動小数点数が

となるときである。

つまり小さい数については、 までの値を正確に表すことができる。整理すると、

となる。