双曲線
概要
双曲線とは、
双曲線の方程式は、右辺が
で表される。
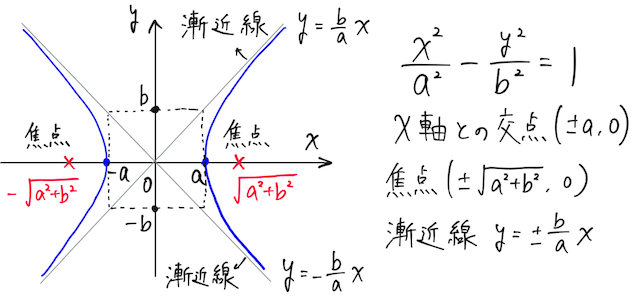
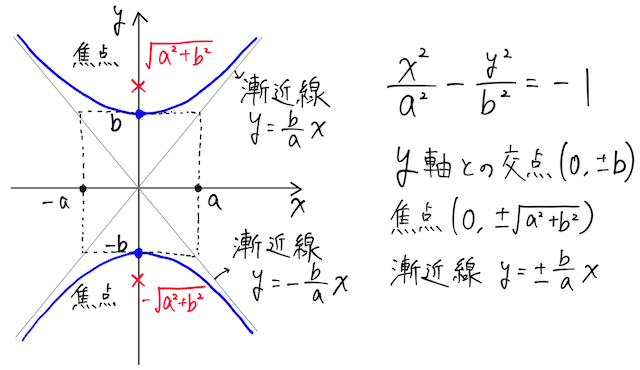
双曲線上の接点
で表される。
証明
双曲線の方程式の厳密な証明は、例えばAKITOさんの動画やただよび・高瀬先生の動画を参照。よく同値性が誤魔化されている証明が載っているので、注意。
ここでは、1つ目の双曲線の形で接線の方程式を証明する。
双曲線の方程式を両辺
(この微分は、合成関数の微分を用いている)
よって、
となる。接線の方程式の作り方をポッカリ忘れた方は、この「接線の方程式」の辞書で確認。
いま、
を得る。
また、
補足
双曲線の媒介変数表示は、「円の媒介変数表示」の辞書の補足で確認しよう。
軸との交点は、覚えていなくても
上では、双曲線の中心が原点にある場合のみを扱ったが、中心が違うところにある場合もある。その場合は、中心の移動に応じて、全部平行移動すれば問題ない。
接線の方程式は、円の場合と同じように、
関連動画






