概要
放物線は、これまでも散々やってきたが、高校数学の最後の最後に新たな定義が登場する。
放物線は、 つの点(焦点)と つの線(準線)からの距離が等しくなるような点の集合と定義される。
方程式は、 軸方向に広がるものと、 軸方向に広がるものがあり、それぞれ以下の通り。
後者は変形すると、これまでにやってきた親しみのある放物線の式
が姿を表す。
軸方向に広がるものは、以下の通り( として書いているが、 の時は左右がひっくり返る)。
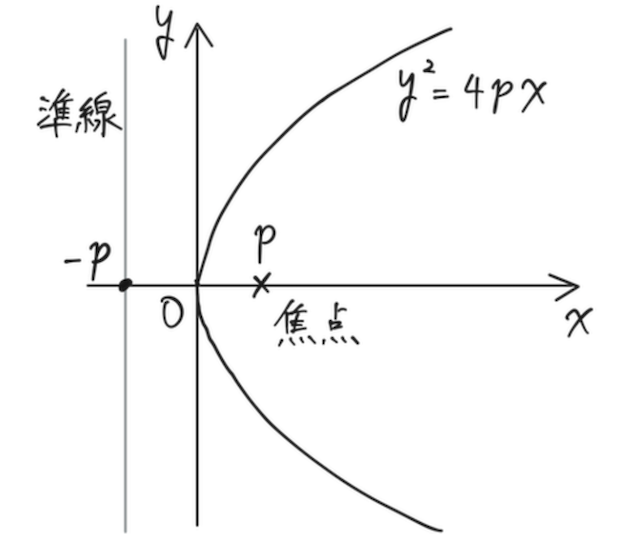
軸方向に広がるものは、以下の通り( として書いているが、 の時は上下がひっくり返る)。
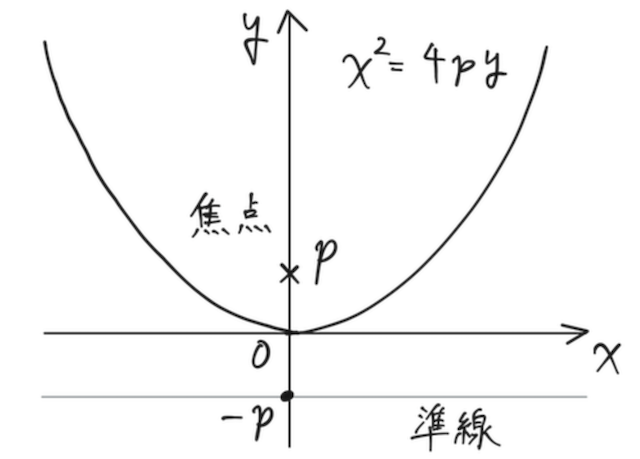
放物線上の接点における接線の方程式は、それぞれ以下の通り。
証明
軸方向に広がるものの場合で、接線の方程式を証明する。
放物線の方程式を両辺 で微分すると、
(この微分は、合成関数の微分を用いている)
のとき、
よって、 における接線の方程式 は
となる。接線の方程式の作り方をポッカリ忘れた方は、この「接線の方程式」の辞書で確認。
いま、 は放物線上にあるので、代入して、
を に代入して、接線の方程式
を得る。
また、 のとき、つまり、点 での接線は、 で表されるが、この接線の方程式に含まれる。
補足
上では、放物線の頂点が原点にある場合のみを扱ったが、中心が違うところにある場合もある。その場合は、中心の移動に応じて、全部 平行移動すれば問題ない。








