コンプトン効果

コンプトン効果の背景

受験界（の一部）で、青チャートをやるべきか否かが白熱して議論されているように、現代物理学の世界では、光が波なのか粒子なのか、というテーマについて様々な議論が行われてきた。

光は粒子だ、という立場の歴史は、

• 19世紀後半：光電効果の発見
• 1905年：アインシュタインが光量子仮説を提唱し、光電効果を説明
• 1916年：ミリカンが実験により光量子仮説を証明

という流れで来ていて、そこで、光の粒子性を説明する光量子仮説を確実なものにしたのが、1922年のコンプトンの実験であった。

コンプトンさんは何を見つけたかというと、X線（可視光線よりもだいぶ波長の短い光）を物質に当てて散乱させると、散乱されたX線の中に、元のX線よりも長い波長のものが含まれる、という事実だった。この事実をコンプトン効果という。

これは、X線が波だと考えると説明がつかず、光が粒子であることの強い根拠となった。

さらに、アインシュタインが光量子仮説として提唱していた光子のエネルギーと運動量の式を用いて、X線を衝突させた際のエネルギー保存則と運動量保存則を立てることで、実験結果と合う式となることを示し、アインシュタインの光量子仮説の根拠となったのである。

コンプトン効果の式

では、電子にX線を衝突させて、どれくらい波長が変化するのかの式を導いてみよう。

元のX線の波長を 、元の方向から角度 の方向へ散乱したX線の波長を 、電子の質量を 、衝突後の電子の速さを 、真空中の光の速さを 、プランク定数を とすると、結論としては、

が成り立つ。

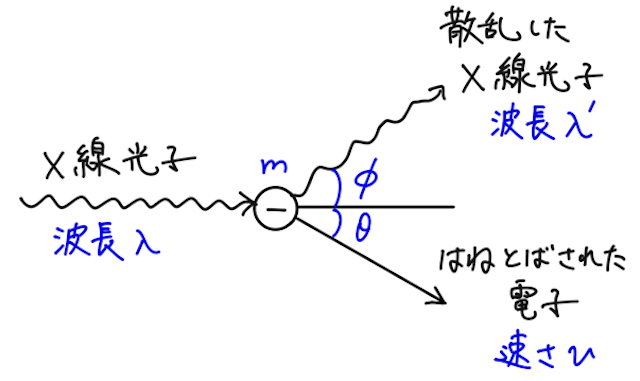
上で書いた通り、これはエネルギー保存則と運動量保存則から導けるので考えていこう。電子は元のX線の入射方向から の方向にはね飛ばされるとする。

まずはエネルギー保存則について。

アインシュタインの光量子仮説で 光子のエネルギー を考えると、

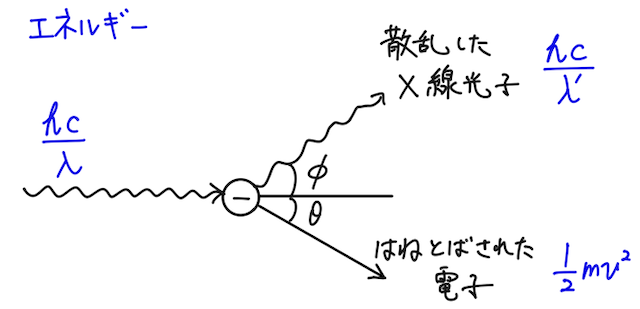
衝突前後のエネルギーの間には、

が成り立つ。入射したX線のエネルギーの一部が、はね飛ばされた電子の運動エネルギーに変わったイメージ。

次に、運動量保存則についても、同様にアインシュタインの光量子仮説で 光子の運動量 を考えると、

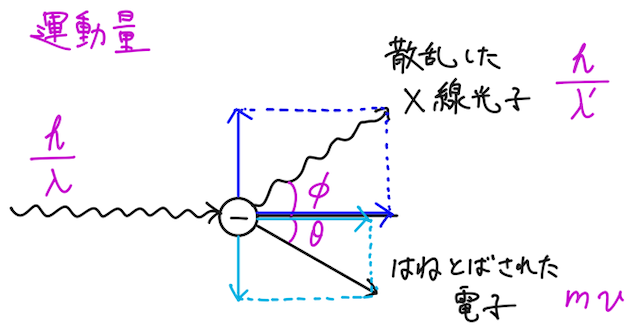
X線の入射方向の運動量については

X線の入射方向に垂直な方向の運動量については

が成り立つ。

〜 より、 と を消去していく。

式より、

となるので、どちらも2乗して足すと、 より

が導かれる。右辺を展開して整理すると、 より

となる。（これで は消せた！あとは を消すのみ）

ここで、 式より

なので、 式に代入して を消去すると

を得る。これを整理していくと、

両辺に を掛けて、

が導かれる。

ここで、 と は非常に近い値であることから、

と考えると、

となって、コンプトン効果の式が導かれた。