区分求積法

概要

シグマによる値の和の極限を、積分によって求めることができるというのが、区分求積法のすごいところである。

同時に、式に圧倒されるランキングでも上位にくるが、これは式をまるごと覚えるよりも、 左辺の式がなぜ右辺と等しくなるかをグラフで理解した方が 倍使えるので、下の例で確認する。

例

を求める。このような、 個の和の極限が聞かれていたら、区分求積法が怪しい。

まず、このような数列の和が出てきたら、、つまり が作れないかと考える。そうすると、

と変形できる。ここで、 の部分を に置き換えて、関数 を考える。

そうすると、この値は、

と書き換えられる。この極限の中身は何を表すかというと、下のグラフの短冊状の面積の和（黄色の部分）になる。

（ 短冊の横の長さが で縦の長さが 、、、 であるため）

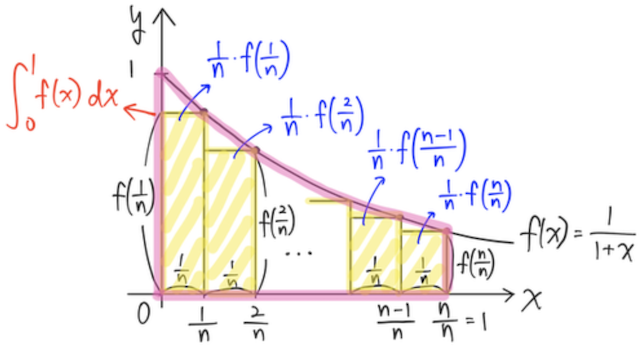
そして、この値の極限（）とは、短冊の 軸上の範囲を 〜 で固定したまま、 この短冊の幅をめちゃめちゃ細かくしていくことなので、 赤の面積に近づいていく。

この赤の面積こそが、区分求積法の右辺である、

になるのである。そしてめでたく計算ができて、

最後は 分の の積分。

補足

左辺が以下の形（シグマの開始と終了が 少ない）でも、同じ変形ができる。

この場合は、短冊の横の長さが で縦の長さが 、、、 となるが、極限をとると、結局上と同じ面積を表していて、同じ積分の値になる。