二体問題
概要
2つの物体が互いに力を及ぼし合いながら運動する物体系の運動は、難関大の入試問題などでよく登場し、二体問題と呼ばれる。
それぞれの物体の運動方程式を立てれば、原理的には解けるっちゃ解けるものの、処理が少し複雑になる。
実はそれぞれの運動を調べる代わりに、重心運動と相対運動に分けて考えることで、式の処理がラクになることが多いので、発展的ではあるもののその概要を学んでみよう。数式がたくさん登場するものの、数学的に難しいことをしているわけではないので、丁寧に式を追っていこう！
物体系ってなんじゃ、外力ってなんじゃという方は、先にこの運動量保存則の辞書で定義を確認しておこう。
以下の内容
- 重心運動方程式
- 相対運動方程式
- 重心運動エネルギー
- 相対運動エネルギー
- 衝突のエネルギー損失
動画の方がわかりやすい、という方は、
を見てみよう。実際に問題を解く際の使い方も学べる。
重心運動方程式
質量
物体1には、
- 物体2から受ける内力
- 物体系の外から受ける外力
（複数の力を受けていたら、その合力）
物体2には、
- 物体1から受ける内力
- 物体系の外から受ける外力
（複数の力を受けていたら、その合力）
がはたらいているとする。
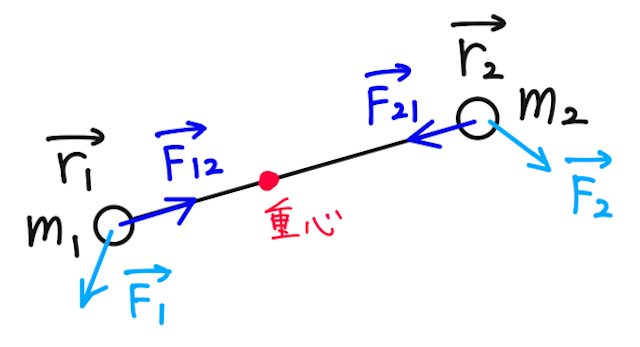
このとき、物体1, 2それぞれの運動方程式は、
と表せる。
ここで、物体1, 2からなる物体系の重心がどのような運動を行うのか、つまり重心の運動方程式を考えよう。（この「重心」というのは、そこに何か別の物体があるわけではなく、そういう位置を仮想的に考える、というものなので注意）
物体1, 2からなる物体系の重心の位置
重心速度
すると、
となる。ここで、物体系の全質量を
なので、
と表せる。さらに、作用反作用の法則より、物体1, 2の間にはたらく内力について
が必ず成り立つので、
を得る。これを重心運動方程式という。大事なのは、左辺は全質量に重心加速度がかけられた形であることと、右辺が外力のみとなっているところ。つまり、全質量が重心に集まっているとして、物体にはたらく外力のみを考えた運動方程式を考えれば良いということになる。
よって、外力がはたらかず、内力のみがはたらく場合には、重心加速度は0となり、重心速度は一定となる。 試験問題でも、この考え方が役に立つことが多い。
相対運動方程式
物体系の運動のうち、重心の運動については上の重心運動方程式を解くことによって考えることができる。しかし、重心の運動だけでは物体系の運動を完全に表せたとは言えない。なぜなら、例えば重心の周りで振動していたりと、重心が運動していなくても、2つの物体が運動していることがありうるからである。
そこで、重心から見た物体系（重心系）の運動を考えることにする。重心から見た物体1, 2の相対位置を
となる。
※ 相対速度の考え方と同じで、観測する対象マイナス観測者で求められる。
上で定義した重心の位置の式から、
となるので、重心から見ると、2物体は一直線上を運動していることになる。すると、これらの2物体がどれくらい近づいているか、どれくらい離れているかの位置情報がわかればいいことになるので、物体1から見た物体2の相対位置
そのためには、物体1から見た物体2の相対加速度
ここで、作用反作用の式
と変形できる。ここで、
なので、この逆数を両辺にかけて変形すると
となる。このとき、左辺の相対加速度にかかる係数
のことを換算質量という。次元を考えると、質量と同じ次元を持つことがわかる。
この式を、式のまま眺めてみると、質量
重心運動方程式が外力のみに依存していた（つまり重力の運動は外力のみに影響を受ける）のに対し、2物体の相対的な運動は内力にも影響を受けることに留意。試験問題では、物体系に外力がはたらくことは珍しく、外力がはたらかなければ、右辺が内力だけになって、相対運動方程式はもうちょいスッキリする。
まとめると、
- 重心運動方程式
- 相対運動方程式
重心運動エネルギーと相対運動エネルギー
上では重心運動と相対運動の運動方程式を考えたが、運動エネルギーはどうなるだろうか。実は、2物体の運動エネルギーの総和は、重心運動に関するエネルギーと相対運動に関するエネルギーに分離できる。 このきれいな事実を、以下確認しよう。
ここが、物理が得意な人が興奮して鼻血を流しがちなところになる。
上と同じ設定で、重心速度
の式を変形すると、
ここで、物体1から見た物体2の相対速度を
となるので、それぞれの物体の速度を重心速度と相対速度で表すことができ、
となる。よって、2物体の運動エネルギーの総和は、
ときれいに変形できる。このとき、最後の行の1項目は、全質量と重心速度を用いた重心運動に関係するもので、重心運動エネルギーと呼ばれる。2項目は換算質量と相対速度を用いた相対運動に関係するもので、相対運動エネルギーと呼ばれている。
よって、2物体の運動エネルギーの総和は、重心運動に関するエネルギーと相対運動に関するエネルギーに分けて考えることができることが示された。
何が嬉しいかというと、例えば物体系に外力がはたらかない、つまり重心速度が一定となる運動では、重心運動エネルギーは変化しないので、相対運動エネルギーの変化のみ考えれば良いことになって、式がとてもシンプルになる。例として、下の衝突の場合でありがたさを確認しよう。
衝突のエネルギー損失
直線上の衝突を考える。質量
衝突によって物体が及ぼしあう力は内力であるので、重心運動エネルギーは衝突の前後で変化しない。変化するのは相対運動エネルギーのみであるから、その変化を調べればOK。
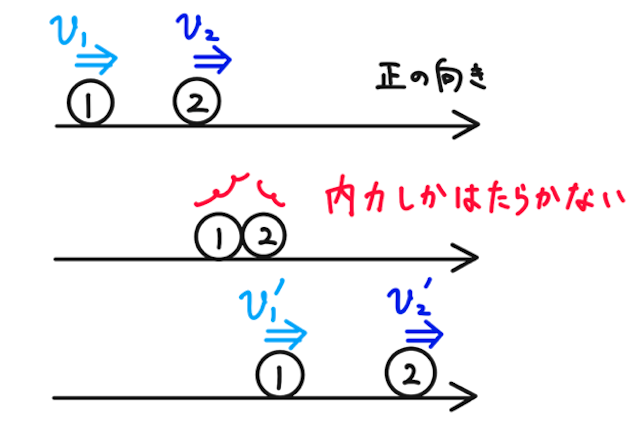
衝突前の速度を
として、
と表される。ここで、反発係数の式は
であるから、
となるので、
と簡潔に求められる。
これを、地道にそれぞれの物体の衝突後の速さを求めて、運動エネルギーの変化を求めて、、、とやっていると結構計算が大変なので、一度やってみて、相対運動で考えることのありがたさを実感しよう。
また、この失われた運動エネルギーの式から、次の大事な事実がわかる。
つまり弾性衝突のとき、 つまり物体系の運動エネルギーは失われず保存する つまり非弾性衝突のとき、 つまり物体系の運動エネルギーは失われ、保存しない
※ 弾性衝突のときでも、物体1つ1つの運動エネルギーは基本的に変化しているので注意！物体系で合計すると保存する、ということ。