ビオ・サバールの法則
概要
電流が作る磁場の式については、高校物理では以下の代表的な3パターンを「覚えるもの」として扱われることがほとんどである。
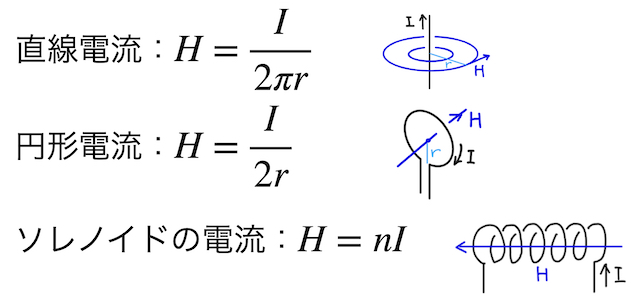
理由としては、この辞書のテーマであるビオ・サバールの法則や、大学で学ぶ線積分という数学的道具が必要になるためであるが、雰囲気だけであれば高校数学の内容でも十分理解できるので、電流が作る磁場の式の背景が知りたくて眠れない方は、下の詳細を見てみよう。
そんなに興味がない人は、「なんかハリーポッターの呪文にありそうな公式で示せるんだな」とだけ覚えて、上の公式は丸暗記しよう。
結論から言うと、ビオ・サバールの法則というものを用いると、電流がある位置に作る磁束密度ベクトルを式で求めることができる。 電流素片
で表される(微分形)。これは、ビオさんとサバールさんが実験により得た法則。
この法則の使い方のイメージは、電流の微小部分を取り出し、それが位置
詳細
では、少し法則の中身を見ていこう。
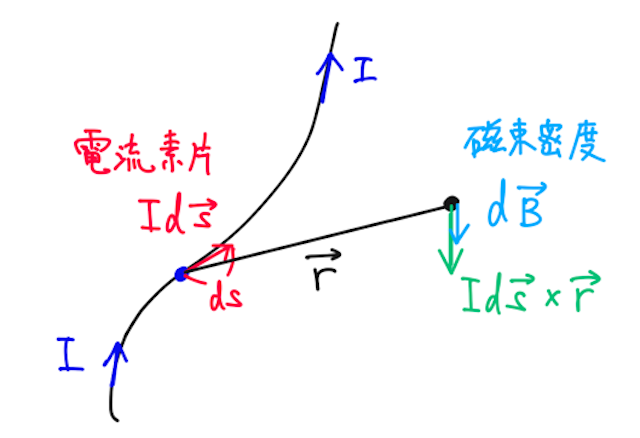
「電流素片」
- 大きさは
(スカラー量) - 向きは、
から へ右ねじを回したときに、ねじが進む向き
となるベクトル量を表す。(外積についてはここでは詳しく扱わないので、知らない方はガチノビさんの動画を見てみよう。)
最後に足し合わせるときは、電流に沿って足しあげるのだが、それはつまり数式で言うと、
では、具体的な公式を導出しながら、ビオ・サバールの法則の使い方を学んでいこう。(以下、単に「磁束密度」と書いたら、それはベクトルだと認識しよう)
①直線電流が作る磁場の導出
まずは無限に長い直線電流が作る磁場について。
下の図のように、直線電流
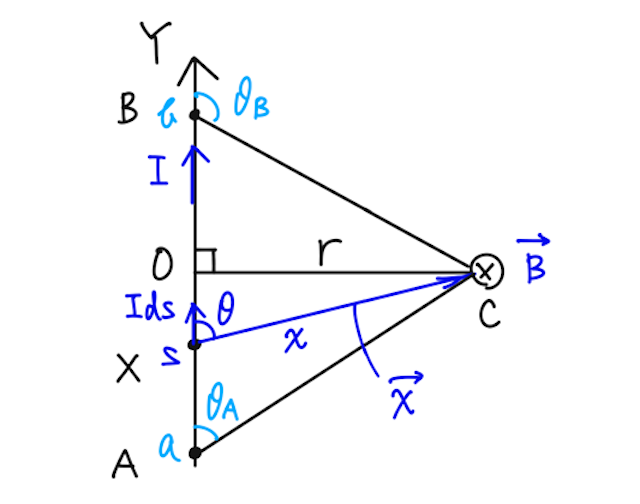
まず、どの点の電流素片を考えても、
あとは磁束密度の大きさ
まずは、線分AB間の電流が点Cに作る磁束密度の大きさ
である。これを電流の方向、つまり線分AB間で足し上げていけば良いので、求める磁束密度の大きさ
で求められる。(
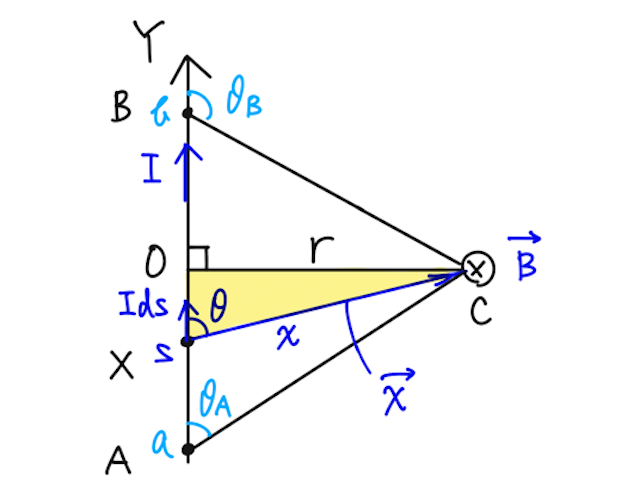
ここで、
また、
(
を得る。(三角関数の導関数の辞書はこちら)
ここで、
となる。(
②円形電流が作る磁場の導出
次は円形電流がその中心軸上に作る磁場について。
下の図のように、円形電流
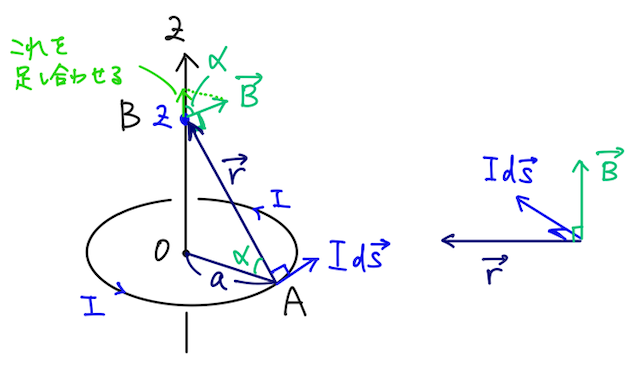
まず、円形電流上の電流素片を考えて、
あとは磁束密度の大きさ
上の図の点Aでの電流素片が点Bに作る磁束密度の大きさは、
となる(
この中心軸成分は、
と求められる。あとは、電流の方向、つまり円に沿ってこの値を足し上げれば点Bでの磁束密度の大きさが求められて、
を得る。
(厳密には大学で学ぶ線積分が必要だが、「
よって、円形電流の中心Oでの磁束密度の大きさは、
となる。(
③ソレノイドコイル内の磁場の導出
では②の円形電流の議論を使って、最後に、半径
中心軸上に、以下のように点Oを原点とした
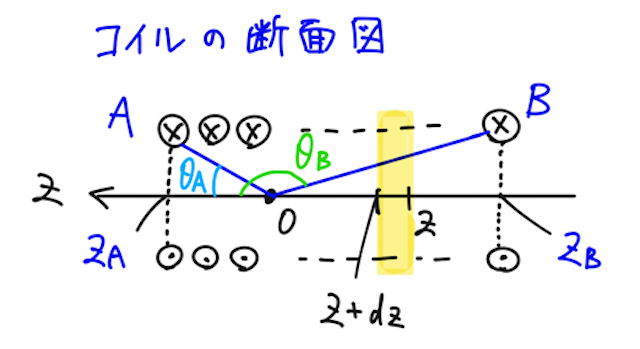
座標
となる。(注:本来は分母の
これを、
となる。(点Oを動かしているわけではなく、あくまでもコイル全体が点Oに作る磁束密度の大きさを求めている点に注意)
ここで、
と置換すれば、この積分はスルッと計算できる。
なので、(三角関数の導関数の辞書はこちら)
と求められる。(コイルの半径
となって、中心軸上の位置によらない値となる。(
ちなみに、今回は中心軸上で考えたが、コイル内であれば中心軸上であってもなくても磁場は等しくなる。
補足
ビオさんとサバールさんは、どっちもフランス人だが別人。たまに、ビオ・サバールという人だと勘違いしている人がいるので、気をつけよう。
また、フランスっぽくおしゃれに「ビオ・サヴァール」と書かれることもある。
この用語を含むファイル
関連動画