放物線の面積公式
概要
放物線
と直線
の交点の
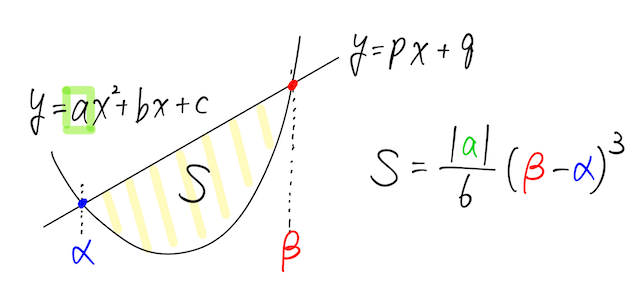
また、放物線
と接線
の接点の
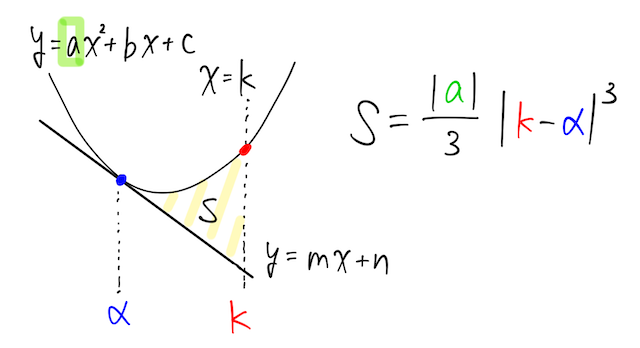
さらに、放物線
と
ちなみに、この
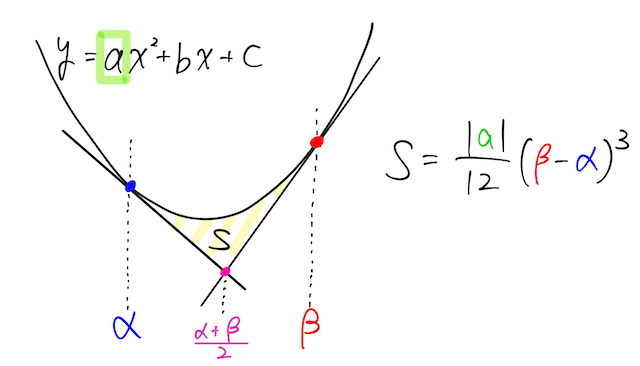
証明
例として、
下の★の値が
なお、証明の式変形に出てくる「1次式のn乗の積分」の辞書はこちら。とても使える技!
補足
- 「
分の 」公式の詳しい証明動画は、たとえばヨビノリさんの証明動画、古賀真輝さんの証明動画、AKITOさんの証明動画などを参照 - より発展的な 「見方」 はガチでノビる受験数学さんの動画を参照
つ目の公式を「 分の 公式」、 つ目の公式を「 分の 公式」と呼ぶことも多い。 - 実は「
分の 公式」と呼ばれる公式には、 あと パターンあって、気になる方はこの河野玄斗さんの動画を参照。 次関数バージョンはこちらの「1次式のn乗の積分」の辞書でも確認できる。 - これらの式は、 覚えておかないと解けないことはないが、覚えていると時間を短縮できたり、答えが合っているか確認できる、という必殺奥義的なもの
関連動画
関連用語





