1次式のn乗の積分
概要
ここでは自然数
細かく言うと、この式自体も数学IIIの範囲とされるものの、
下の例の通り、
ちなみに、
例
【簡単編】
ただし、
【応用編】
この
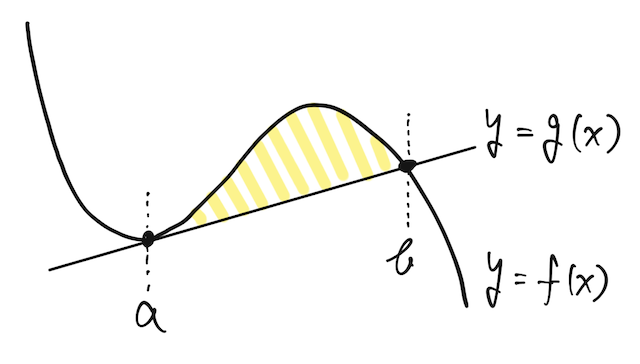
例えば、上の
と表される。ここで一工夫。積分の中身について、実は、因数定理から、
と因数分解できるので、定積分の式は
となって、上の例題の式が登場し、
補足
係数については計算ミスが起きやすいので、初めのうちは逆算(微分)をして元に戻ることを確かめると確実。
この用語を含むファイル
関連動画
ここでは自然数
細かく言うと、この式自体も数学IIIの範囲とされるものの、
下の例の通り、
ちなみに、
【簡単編】
ただし、
【応用編】
この

例えば、上の
と表される。ここで一工夫。積分の中身について、実は、因数定理から、
と因数分解できるので、定積分の式は
となって、上の例題の式が登場し、
係数については計算ミスが起きやすいので、初めのうちは逆算(微分)をして元に戻ることを確かめると確実。
この用語を含むファイル
関連動画