概要
道順の問題は、一見何の分野の問題なのかわからないが、一時期大流行したダンスダンスレボリューションのようなイメージで、 「→」「↑」の並び替えと考えると、場合の数の問題になる。「→」は右に一マス、「↑」は上に一マスという意味。左とか下に行ってしまうと、最短経路にならなくなる。（もちろんスタートが左下ではない場合は別）
よく 「最短経路問題」 とも呼ばれるが、現実では碁盤目状の道があるのは、京都や札幌くらいで、我々の手にはGoogle Mapがあるので、あまり現実世界では役立たないように思う。
例
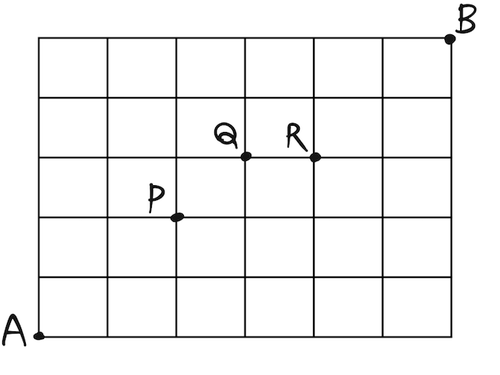
図のような道のある町で、 から までの最短経路のうち、次のものの総数を求めよ。
最短経路すべて
を意地でも通る
道 が工事中で通れない
「→」 個、「↑」 個の並び替えと考えて、
で 通りと求められる。
から までの道順は、「→」 個、「↑」 個の並び替えと考えて、
なので 通り。 から までの道順は、「→」 個、「↑」 個の並び替えと考えて、
なので 通り。これらの道順は独立なので、掛け算ができて、
で 通りと求められる。
余事象で考える。つまり、全体の道順の数から、 を通ってしまう道順の数を除けば良い。 を通ってしまう道順の数は、 と同様に掛け算で考えることができる。
まずからまでの道順は、「→」個、「↑」個の並び替えと考えて、
なので 通り。 から までの道順は 通り。 から までの道順は、「→」 個、「↑」 個の並び替えと考えて、
なので 通り。これらの道順は独立なので、掛け算ができて、
で 通りと求められる。よって、 で求めた全体から引いて、
で、 通りと求められる。
補足
ここでは解説しなかったが、中学入試などでよく用いられる「書き込み方式」も威力を発揮することもある。
