独立な確率変数

概要

つの確率変数 、 が独立であるとは、 のとりうる任意の値 と、 のとりうる任意の値 に対して、

が成り立つことをいう。イメージとしては、確率変数がある値をとる確率が、相手の値によらないということ。（言葉が難しくなっただけで、数学Aの場合の数・確率分野で学ぶ「独立」と同じことを言っている）

「任意の」、つまり「全ての」というのがポイント！この等号が成り立たないような値の組み合わせが つでもあれば独立ではない。

独立であるかを調べるには、基本的には、この定義に沿って、全ての値の組み合わせで等号が成り立つかを確かめていくことになる。

独立な確率変数の例

まず初めに、独立な確率変数の例を確認してみよう。

確率変数 、 のとりうる値とその同時分布が以下の通りだとする。（お互いに つの値をとりうる場合を考えている）

※「同時分布」とは、こんな感じで つ以上の確率変数の対応をまとめたもの。

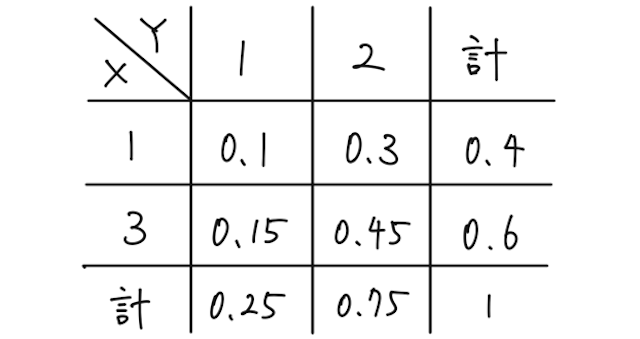
では、例えば 、 となる確率について考えてみよう。上の表より、

• （← の値は何でもよく、とにかく となる確率）
• （← の値は何でもよく、とにかく となる確率）

であるので

となり、

であることがわかる。

さらに、下の図に書き込んだ通り、それぞれの確率変数の他の全ての値同士の組み合わせで

が成り立つので、この確率変数 と は独立である。

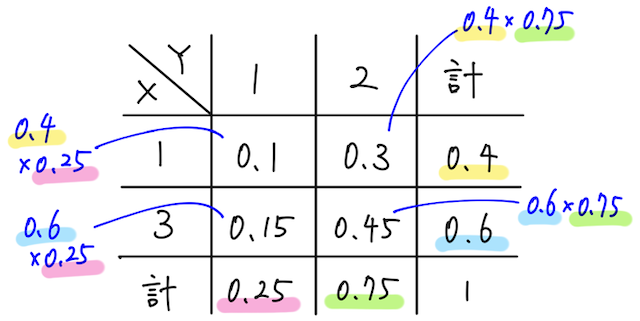
独立でない確率変数の例

では、独立でない確率変数の例も確認してみよう。

確率変数 、 のとりうる値とその同時分布が以下の通りだとする。

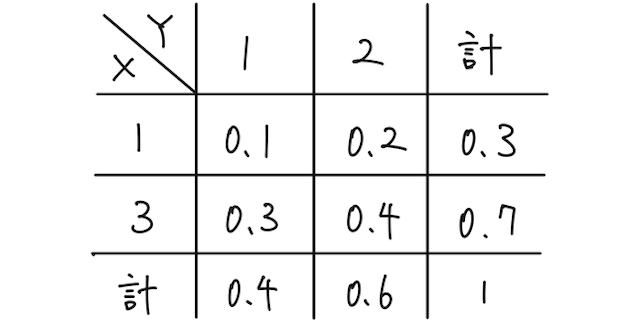
では、例えば 、 となる確率について考えてみよう。上の表より、

• （← は何でもよく、とにかく となる確率）
• （← は何でもよく、とにかく となる確率）

であるので

となり、

であることがわかる。

よって、この確率変数 と は独立でない。（ つの組み合わせでも見つかれば、独立ではない！）

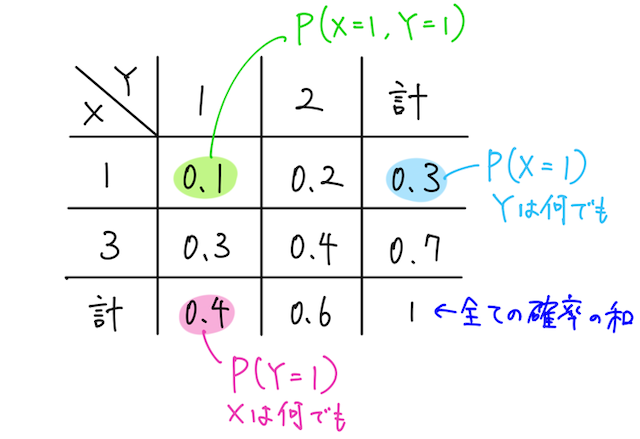
※ ちなみに、他の組み合わせで考えても同様に成り立たない。ぜひ確認してみよう。

独立な確率変数の性質

確率変数が独立だと成り立つ良い性質がいくつかある。例えば確率変数 と が独立であれば、

• 期待値の積が分解できる

• 分散の和が分解できる

※ 確率変数が つ以上でも同様に分解できる。

それぞれ確認・証明してみよう。

期待値の積が分解できる証明

ここでは、確率変数 のとりうる値を 、確率変数 のとりうる値を とおく。このとき、積の確率変数 の期待値は、定義から

となり示される。（ 行目から 行目への変形で、確率変数が独立であることを用いている点に着目しよう！）

分散の和が分解できる証明

分散は「確率変数の 乗の期待値」－「期待値の 乗」で求められることを用いると、

ここで、「和の期待値は期待値の和」なので、

と変形できる。さらに、確率変数 と が独立であるとき、上で示したように

であるので、

となって、示される。

補足

ちなみに、「和の期待値は期待値の和」 の性質

は独立でなくても成り立つので注意。証明を考えれば、特に独立性を使っていないので納得できるはず。

また、 つの確率変数が独立かどうかを調べるには、最初に書いた通り、基本的には定義に沿って全ての組み合わせを検討することになるが、お互いの結果に影響を及ぼさないようなときは明らかに独立であると言えることも多い。

例えば、大小のサイコロを つ投げて、大きいサイコロの目を確率変数 、小さいサイコロの目を確率変数 とおく。このとき、例えば 、 となる確率は

と、それぞれの確率の掛け算で求められることは直感的にわかるはず。（確率の分野で「積の法則」と呼ばれているもの）

つまり、お互いに、とる値の確率に影響を及ぼさないようなときは確率変数は独立であり、この積の関係式が使えるんだ、ということを意識しておこう。