平面ベクトルの和の等式

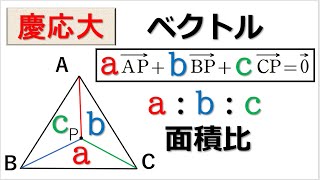
＜問題＞ △ABCに対して， 6\vec{AP}+3\vec{BP}+4\vec{CP} = \vec{0} を満たす点 P を考える. (1) 点 P はどのような位置にあるか. (2) 面積比 △PBC:△PCA:△PAB を求めよ. この動画では、各小問に対してそれぞれ3つの解法を紹介しています。 ＜この動画について＞ ベクトルの等式をから，図形的な情報を取り出すことができるか？ ベクトルの初学者にとって非常に重要な問題だと言えますね！ 「点Pを視点にしてはいけないのですか？」という生徒からの質問に対する答えが (1)の解法3です． これだけ自由にベクトルを扱えたら，もう初心者とは言えないでしょう！ 今日から33日間，毎日投稿をします． シリーズ「ベクトルに捧げる，2020夏。」始動です． ＜関連問題＞ 分点・重心の位置ベクトル https://youtu.be/rS7ERmgmvGg 【むくち解説62秒】メネラウスの定理 https://youtu.be/0aUuk8ExfRg ＜はやくち解説とは＞ かったるい説明に嫌気がさしたときに見る動画。早口×早送りで解説しました。雰囲気を掴んでもらえたらいいと思っています。 ＜目次＞ 00:00 問題説明 00:19 (1) 解1 始点をAに揃える 01:52 (1) 解2 始点をOに揃える 03:18 (1) 解3 始点をPに揃える 04:26 (2) 解1 三角形を経由する 05:49 (2) 解2 始点をB，Cに揃える 07:32 (2) 解3 メネラウスの定理 08:20 今回のキーワード ＜キーワード＞ #平面ベクトル #条件式 #線分の比 #面積の比 #分点公式 #内分点 #位置ベクトル #始点を揃える #差に分解する #高さの比 #底辺共通 #メネラウス #重心座標 ＜使用機材＞ カメラ：iPhone 11 Pro タブレット：iPad Pro 12.9インチ アプリ：Good Notes 5 編集ソフト：Final Cut Pro