円順列
概要
回転して同じものになるものを1通りとカウントするような順列を、円順列という。
異なる
「とにかく1つを固定!」とか「マイナス1して階乗!」などと、呪文のように刷り込んでいる(まれている)方も多いかもしれないが、円順列マスターになるには、
例
男子2人、女子2人が、円形のテーブルに等間隔で座るとき、場合の数は
となる。
公式の理由
例えば、上の例に合わせて、こんな席に4人(A, B, C, D)が座るとする。
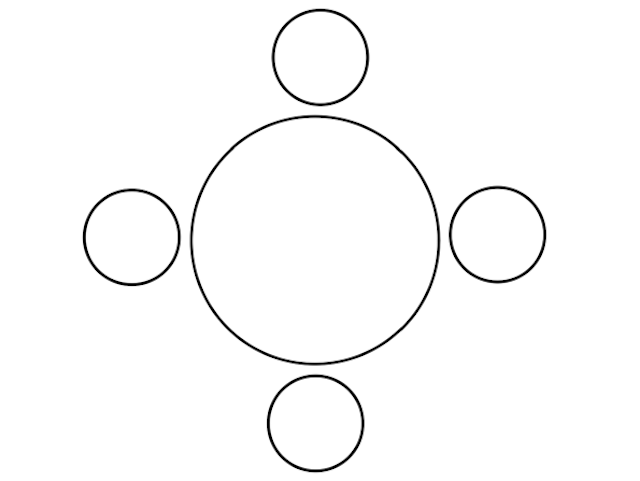
4人の順列なのだから、各席について誰が座るかを考えれば、総数は
となりそう。
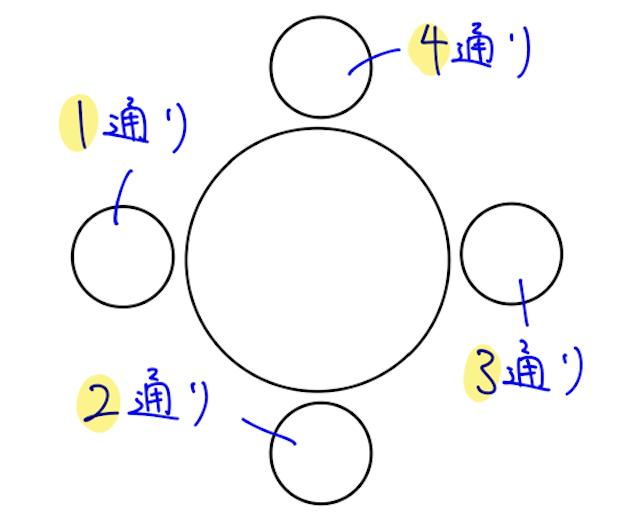
ところが、この24通りの中には、例えば下のような4通りが含まれている。
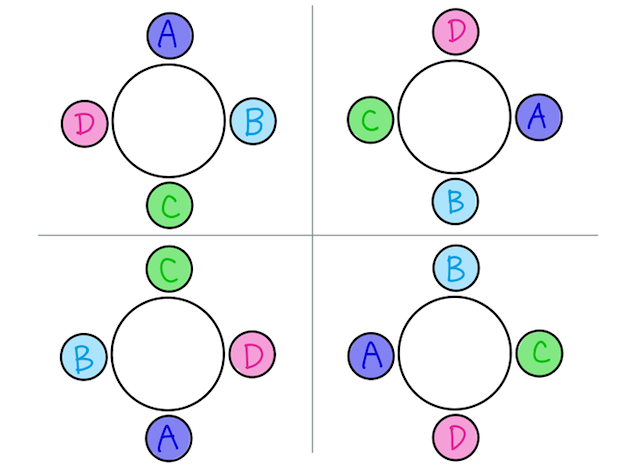
実はこれらの4つは、回せば同じ形になっているので、円順列を考える際には同じものとみなされ、1通りとカウントしないといけない。
24通りの総数の中には、このように4つずつ「回転して同じになるペア」があるので、円順列の場合の数は、
となる。
一般化すると、異なる
「1つを固定」とは
「1つを固定して残りを並べよ!」というフレーズを聞いたことがある方も多いと思うが、これは、1つをどこかに固定すれば、(平面の場合は)上のような回転して同じになるものが出てこなくなるので、残りのものを自由に並べる順列を考えればよくなるし、それで漏れなく数えられるよね、という作戦。
とても便利なので、理由をしっかり押さえた上で考え方を押さえておこう。
最初の例だと、例えばAくんを上の席に固定して、B〜Dの座り方として
と求められる。
補足
でもテーブルって普通四角じゃない?円形とかニトリでしか見たことないんですけど。という方も多いと思う。
四角形のテーブルに座る順列だとどうなるかを考えることで、円順列の理解がとても深まるので、興味のある方はこの 福田次郎さんの演習動画 を見てみよう。
関連動画
関連用語




