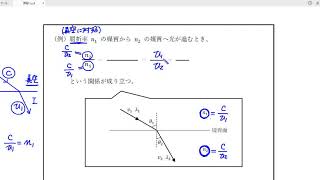
概要
波が、異なる つの媒質の境界面を斜めに入射するとき、波の進行方向が急に変わる。この現象を波の屈折という。
入射角と屈折角は、下の図のように定義される。
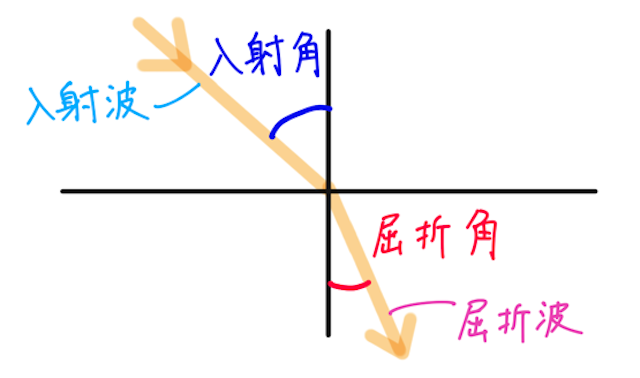
ここで、入射角を 、入射波の速さを 、波長を とおく。他方、屈折角を 、屈折波の速さを 、波長を とおく。
このとき、次の式が成り立つ。
これを屈折の法則という。
このとき、この比の一定値を、媒質 に対する媒質 の屈折率(相対屈折率)といい、 で表す。「どっちに対するどっちの屈折率」なのかの定義と、添字の順序を忘れないようにしよう!むちゃくちゃ紛らわしいけど、定義様には逆らえない。
ホイヘンスの原理による説明
ここでは、ホイヘンスの原理を用いて、屈折の法則を説明しよう。
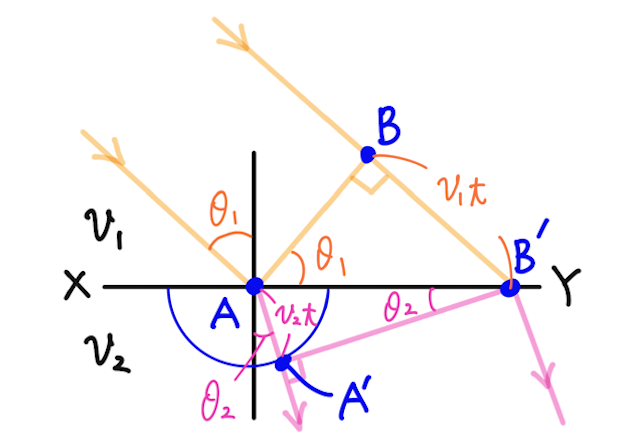
入射波を伝える媒質を媒質 とし、この中での波の速さを 、屈折波を伝える媒質を媒質 とし、この中での波の速さを とする。
上の図のように、境界面 に対して入射角 で速さ で入射する平面波を考える(オレンジの波)。波面と波の進行方向は垂直なので、 は波面となる。
上の に入射した波は、直後に から素元波を発生させる。その時点で点 にある波が、その後 上の点 に到達するまでの時間を とおくと、その間に から出た素元波は、半径 の半球面を描いている。(青の半球面)
このとき、境界面 の間の各点を波源とする素元波も、それぞれ半球面を描き、それらの共通に接する面が、屈折波(ピンク)の波面となる。それが である。(何言ってるかわからない人は、ホイヘンスの原理から復習しよう)
よって、 と に注目すると、
となる。
さらに、波の振動数 は屈折の前後で変化しない(波長は縮んだり伸びたりするが、例えば山の個数などは変わらない)ので、波の基本式から、
となる(ただし、媒質 での波長を 、媒質 での波長を とした)。これで屈折の法則が導かれた。
絶対屈折率(光波の場合)
上で、媒質 に対する媒質 の 屈折率(相対屈折率) を定義したが、ややこしい言葉として、媒質の絶対屈折率という概念がある。
これは、 光波を考えた場合に登場する概念で、真空に対する媒質の相対屈折率のこと。
上の例を使うと、媒質 が真空の場合の媒質 の屈折率が、媒質 の絶対屈折率で、 と表す。 単に「屈折率」と呼ばれることもある。このとき、光の速さを とおくと、屈折の法則より、
となる。
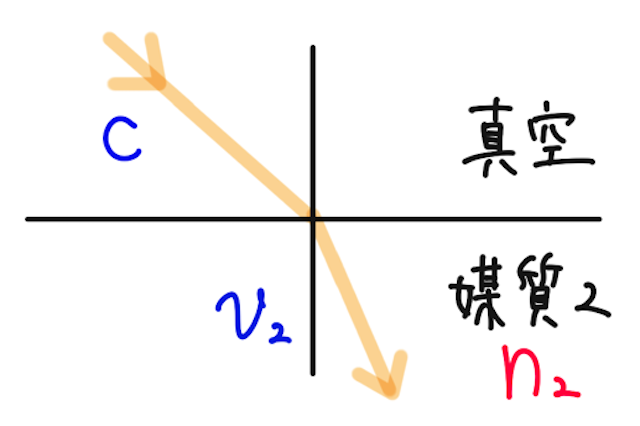
もちろん媒質 の絶対屈折率を考えることもできて(真空中から媒質 に屈折するような波を考えれば良い)、それを とおくと、同様に
となるので、
が成り立つ。よって上で導いた屈折の法則とまとめると、
となる。 に関してだけ、添字がひっくり返るので注意。上で見た定義と導出を頭に入れておくと忘れないし、あとは分母をはらった
で覚える人も多い。これだと同じ添字が同じ辺に来るので、頭に優しい。
補足
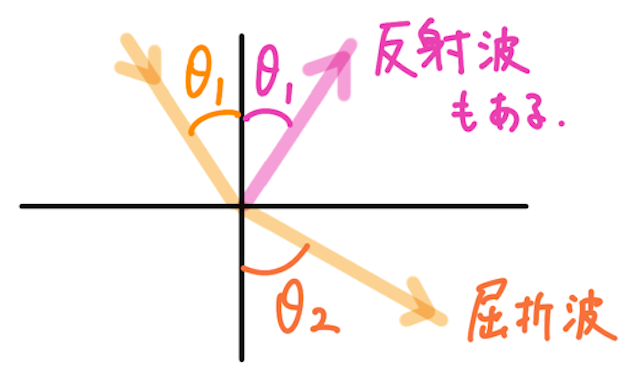
よく勘違いすることとして、波が屈折する(できる)場合には、反射波は存在しないと思いがちだが、実はそうではない。波が屈折するときにも、一部の波は反射している。