仮説検定

概要

仮説検定の考え方は、具体的な例とともに理解した方がわかりやすいと思うので、この問題を考えてみよう。

独特の考え方をするし、専門用語もたくさん登場するので、最初はほんとにとっつきにくいが、何がしたいのか、何が言えたのか、をしっかり考えながら理解していこう。慣れればワンパターン。

例題

あるサイコロを $6$ 回投げたところ $6$ の目が $4$ 回出た。そこで、「このサイコロは $6$ の目が出やすい」と判断できるかどうかを仮説検定を用いて考察せよ。ただし、有意水準を $5$ %とせよ。

考え方の全体像

では、まず考え方の全体像と仮説検定の「キモチ」を詳しく紹介する。ややこしい人は、下の実際の計算例から確認しよう。

直感で、「いや、$6$ の目めちゃくちゃ出やすいやろ！」と言いたくなるが、それは主観的すぎるので、そこをグッとこらえて、客観的に判断できるようにする、というのがここでの仮説検定の大きな仕事。

気持ちとしては、サイコロを振ってみたら $6$ がたくさん出たので、おや？ということで、「このサイコロは $6$ の目が出やすい」と言えるかを今回調べようとしている。（何を検証しようとしているかをはっきりさせるのが、まず最初に大事なこと）

これを主張 $A$ とする（このような、統計的に積極的に検証したい仮説のことを統計用語で 「対立仮説」 という）。

主張 $A$「このサイコロは $6$ の目が出やすい！」

次に、いやいやそうじゃないよ、という主張も考える。ここでは 「このサイコロは公正である」 つまりどの目も同じくらい出やすいよ、というのを主張 $B$ とする。

主張 $B$「このサイコロは公正である！」

（このような、判断したい主張を考えるために立てられた主張のことを統計用語で 「帰無仮説」 という）

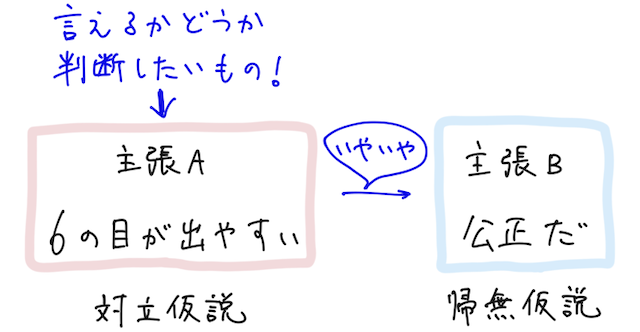
（※ 細かい補足：この解説では、「あくまでも積極的に検証したいのは『対立仮説』の方！」という、仮説検定の「キモチ」を理解するために、あえて対立仮説 → 帰無仮説の順序で書いている。問題などでは、基本的に帰無仮説 → 対立仮説、の順で出てくるので混乱しないように注意しよう）

そして、判断したい方ではない「主張 $B$」（帰無仮説）が成り立つと仮定する。つまり、このサイコロは公正であり、実は $6$ の目が出る確率は $\dfrac{1}{6}$ であると仮定する。

このもとで、サイコロを $6$ 回投げて、今回のように $6$ の目が $4$ 回以上出る確率を考えたときに、その確率が小さく、確かに十分起こりにくいと言えたら、主張 $B$（帰無仮説）を棄却し、主張 $A$（対立仮説）を採用する。つまり、このサイコロは $6$ の目が出やすいと判断する。

逆に、$6$ の目が出る確率が $\dfrac{1}{6}$ だと仮定したときに、サイコロを $6$ 回投げて、今回のように $6$ の目が $4$ 回以上出る確率を求めたときに、結構確率が大きく、起こりやすいと言えるとき、主張 $B$（帰無仮説）は棄却されない。つまり、このサイコロは $6$ の目が出やすいとは言えないと判断する。

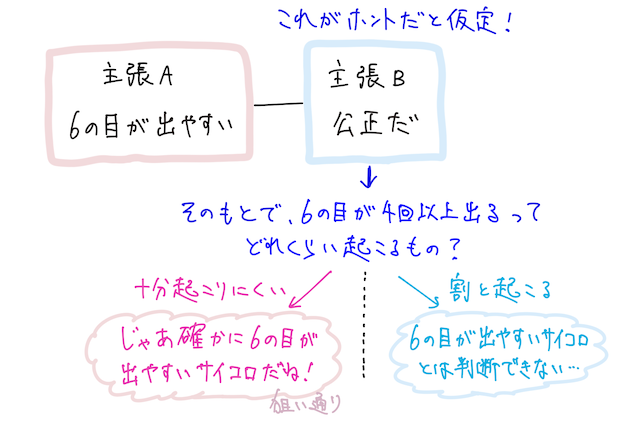
これが仮説検定の流れであり、このイメージが全て。

つまり、もっとざっくりと言うと、公正なサイコロだとしたときに、今回のように $6$ 回投げて $6$ の目が $4$ 回以上出る確率はめちゃくちゃ小さい＝公正なサイコロだった場合そんなことはほとんど起きないじゃん、ということが言えてはじめて、「じゃあ確かに $6$ の目が出やすいサイコロだったんだね、おめでとう」 と認められるイメージ。（帰無仮説を棄却し、対立仮説を採択）

でも、公正なサイコロだとして、$6$ 回投げてそこそこの確率で $6$ の目が $4$ 回以上出るのであれば、「公正なサイコロでたまたま $6$ がたくさん出ただけだったのかもしれないし、$6$ の目が出やすいサイコロだったとは判断できない」という結論になる。（帰無仮説は棄却されない）

注意点として、あくまでも今回は「このサイコロが $6$ の目が出やすい」と言えるかどうかを判断しているので、「このサイコロは公正である」と言えるかどうかは判断できない！

つまり、この仮説検定の結論としては、

• 「このサイコロは $6$ の目が出やすい」と言える（帰無仮説が棄却され、対立仮説が採択された場合）
• 「このサイコロは $6$ の目が出やすい」とは言えない（帰無仮説が棄却されない場合）

の $2$ つのみであり、

• 「このサイコロは公正である」と言える

という結論は得られないので注意！！（気持ちとしては同じじゃんと思うかもしれないが、統計の世界ではこの $2$ つ目と $3$ つ目は大きく異なる。つまり、帰無仮説が棄却されなかったからと言って、帰無仮説の内容を「証明」したわけではないことに注意しよう！ただ矛盾しないことがわかった、というくらいのイメージ。とてもややこしいが、しっかり理解しておこう）

また、上では「ほとんど起きない」とか「そこそこの確率で起こる」とかふわっとした表現を使ったが、じゃあどのくらいの確率以下であれば認めるか、という判断の基準のことを有意水準という。この水準も、検定前にあらかじめ決めておく。計算してみて、結果に応じて都合の良いように設定するのは基本的にNG！

まとめると、一般的に検定の流れはこのようなイメージになる。

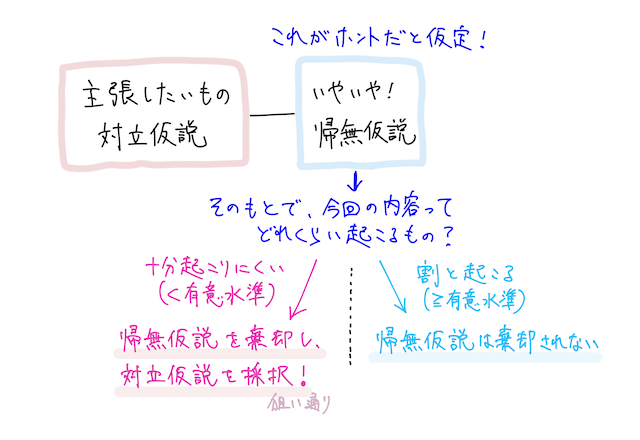
では今回の問題について、実際に計算しながら確認しよう。

実際の検定の流れ

では、上で見た通り、

• 主張 $A$：「このサイコロは $6$ の目が出やすい」（対立仮説）
• 主張 $B$：「このサイコロは公正である」（帰無仮説）

として、「主張 $B$」（帰無仮説）が成り立つと仮定する。つまり、このサイコロは公正であり、$6$ の目が出る確率は $\dfrac{1}{6}$ であると仮定する。

このもとで、このサイコロを $6$ 回投げて $6$ の目が $4$ 回以上出る確率を求める。

• $4$ 回出る確率

$${} _6 \mathrm{C} _4 \left(\frac{1}{6}\right)^4\left(\frac{5}{6}\right)^2=\frac{375}{6^6}$$

※ 後で通分するので、このままにしておく。

• $5$ 回出る確率

$${} _6 \mathrm{C} _5 \left(\frac{1}{6}\right)^5\left(\frac{5}{6}\right)=\frac{30}{6^6}$$

• $6$ 回出る確率

$$\left(\frac{1}{6}\right)^6=\frac{1}{6^6}$$

これらは排反なので、$6$ の目が出る確率が $\dfrac{1}{6}$ であるサイコロを $6$ 回投げて、$6$ の目が $4$ 回以上出る確率は

$$\begin{align} \frac{375}{6^6}+\frac{30}{6^6}+\frac{1}{6^6}&=\frac{406}{6^6}\\\\ &=\frac{203}{23328}\\\\ &=0.0087... \end{align}$$

と求められる。

この確率は、確かに今回の有意水準である $5$ %よりも小さいので、主張 $B$（帰無仮説）を棄却し、主張 $A$（対立仮説）を採用する。

つまり、公正なサイコロだった場合、$6$ 回投げて $6$ の目が $4$ 回以上出る確率が $5$ %より小さいことが言えたので、主張したかったことが認められて、「このサイコロは $6$ の目が出やすい」と言える。

※ もし、計算した確率が $5$ %よりも大きかったら、「このサイコロは $6$ の目が出やすい」とは言えない、という結論になる！