円の方程式

概要

円を表す方程式は、時と場合に応じて つの姿を使い分けできるようになっておこう。標準形と呼ばれる形は、

で表されて、この時、 はこの円の中心を表し、 は半径を表す。

一般形と呼ばれる形は、

で表される。問題を解く上で重要なのは、この つを自由に行き来することと、 「どの場合にどっちを使いやすいのか」 を自分で判断できるようになること。

変形については、一般形から標準形は と それぞれについて平方完成を行えばOK。標準形から一般形も、展開すればOK。

どっちを使うかについては、

• 中心や半径の情報が欲しい時には、平方完成して、一般形から標準形に直す
• 問題文から円の方程式を求めるときは、与えられている情報から、 中心や半径について何かわかる場合には標準形、何もわからなくてつらい場合（通る 点が与えられてたり）は一般形、というのが目安となる

例

【問1】 を直径の両端とする円の方程式を求めよ。

【答1】与えられた情報から、この円の中心と半径がわかる。中心は、この点の中点で、

半径は、この中心と （ でももちろんOK）の距離を考えて、

となる。よって、求める円の方程式は標準形の形を使って、

と求められる。

【問2】 点 を通る円の方程式を求めよ。

【答2】求める円の方程式を、

とおく。（中心は半径がわからないので一般形で設定する）通る 点を代入して

この連立方程式を頑張って解くと、 となるので、求める円の方程式は

となる。

補足

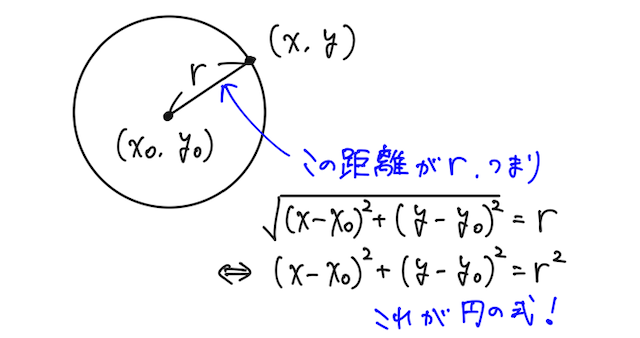
そもそも円の式がなぜこんな形になるかというと、円の方程式は、 ある点（中心） から一定の距離 にある点の軌跡の方程式を表している。

その軌跡上の点を とおくと、 点間の距離の条件から

となって、円の方程式が現れる。