中点公式

概要

$2$ 点 $\mathrm{A},\mathrm{B}$ の中点 $\mathrm{M}$ の位置ベクトルは

$$\overrightarrow{OM} = \frac{\overrightarrow{OA}+\overrightarrow{OB}}{2}$$

で表される（平面、空間どちらでも成り立つ）。足して $2$ で割るだけという、高校数学の公式の中でも、だいぶ頭や心に優しい式。

位置ベクトルなので、基準の点 $O$ はどこでもOK。下では原点として話を進める。

証明

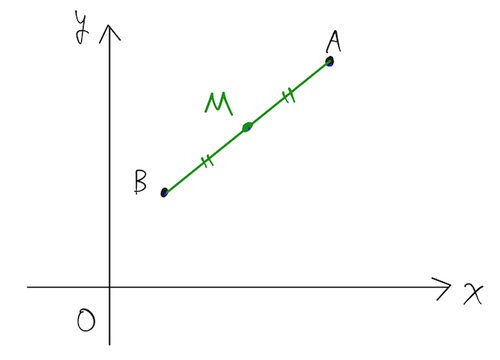
$AB$ の中点 $M$ の位置ベクトルは、

$$\begin{align} \overrightarrow{OM} &= \overrightarrow{OA} + \overrightarrow{AM}\\\\ &= \overrightarrow{OA} + \frac{1}{2}\overrightarrow{AB}\cdots\star\\\\ &= \overrightarrow{OA} + \frac{1}{2}(\overrightarrow{OB}-\overrightarrow{OA})\\\\ &=\frac{\overrightarrow{OA}+\overrightarrow{OB}}{2} \end{align}$$

と表される。（$\star$ は共線条件（つまり中点なのでベクトルも半分）、「共線条件」の辞書はこちらから確認）

平面で書いてるが、空間でも上の式は全く同様に成り立つ。

補足

よく出てくるが、直感的にも思い出しやすい公式。せっかくなので、 成分での計算にも慣れておこう。

$2$ 点 $\mathrm{A} \left(x_{1},y_{1}\right),\mathrm{B} \left(x_{2},y_{2}\right)$ の中点の座標は

$$\left({\frac{x_{1}+x_{2}}{2}},{\frac{y_{1}+y_{2}}{2}}\right)$$

で表される。簡単にいうと、$x$ 座標、$y$ 座標、それぞれ仲良く平均を取ればOK。空間座標の場合は、$z$ 座標も平均をとればOK。

また、この中点公式は複素数平面でも使える（数学III）。つまり、複素数平面上の $3$ 点を $A(z_a),B(z_b)$ とすると、複素数平面上の線分 $AB$ の中点に対応する複素数は、

$$\frac{z_a+z_b}{2}$$

で求められる。