鏡像法

概要

平面や空間内の各点の電場や電位の様子を調べようと思ったら、複数の点電荷によって作られる電場・電位を重ね合わせたり、または一様電場中で考えたり、といった話が高校物理でよく登場する。

一方で、世の中はそんなに甘くもなく、例えば、下の図のように、ある点に置かれた点電荷が、アースした導体の外側に作る電場や電位はどうなる？ みたいなことを考えたいときに、よくわからなくなってしまう。

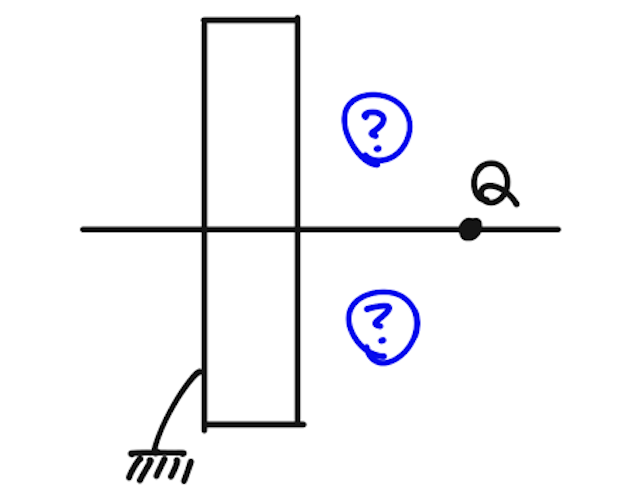
詳しくは、大学物理でポアソン方程式というものを学ぶと、境界値問題を考えることで理論上は求めることができるが、ここでは鏡像法という、パズルチックで実用的な方法で電場や電位の様子を調べる方法を紹介する。

仮想的に電荷を置いて考えるのだが、どこにどういう電荷を置くかはテクニカルなので、「ふ〜ん」と思っておけばOK。

詳細

空間でも考えることができるが、ここでは簡単のため平面上で考える。ここでは鏡像法が役に立つ代表的な問題を考えよう。

として、図のように に電荷 があるとする。さらに、 に側面が置かれてアースされた無限に続く導体も考える。このとき、 に作られる電場や電位の様子はどうなるだろうか。

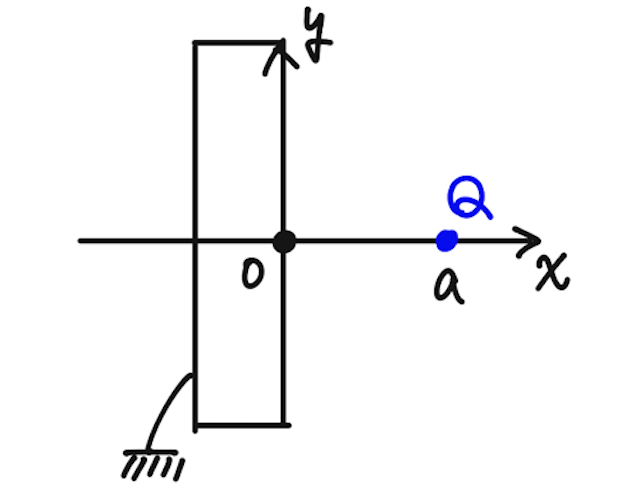
まず、このまま考察してみよう。導体内では自由電子が自由に動き回ることができるため、電場が存在しない。つまり、導体内の任意の2点の電位は等しくなる。今回アースされているので、この導体内の任意の点の電位は0になる。

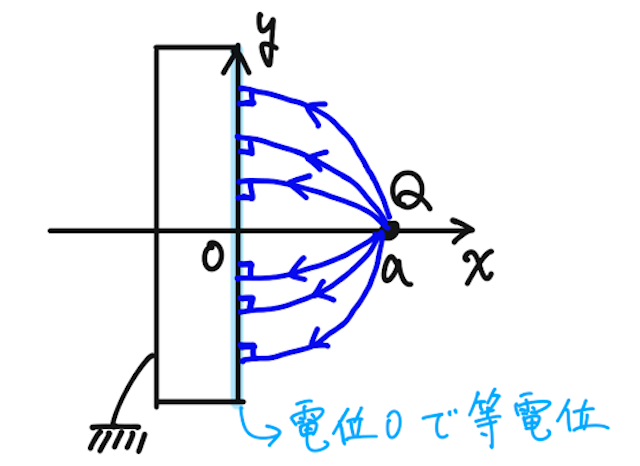
このとき、電気力線の性質から、電気力線は等電位面と直交するので、導体表面に垂直に刺さるはずである。

よって、イメージとしては、こんな電気力線になりそうだとわかる。

ここで、導体をどけて、代わりに に電荷 を置いてみる。

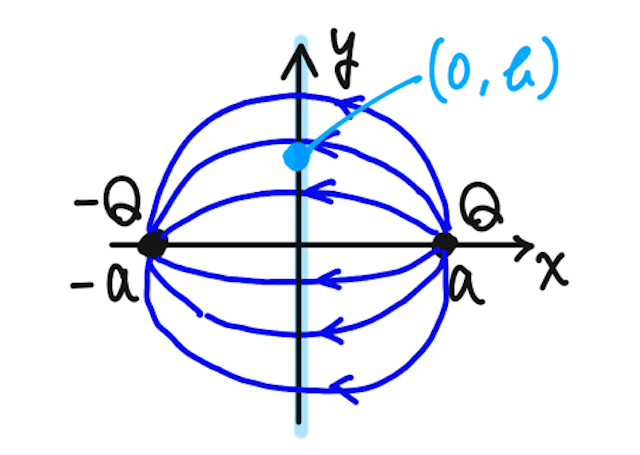
このとき、 上の点 での電位を求めると、点電荷による電位の式より、

電荷 による電位が

電荷 による電位が

なので、足し合わせて電位が0になる。（ の値によらず電位が0）

よって、この場合でも 上では電位0で等電位になっている。つまり電気力線も直交している。

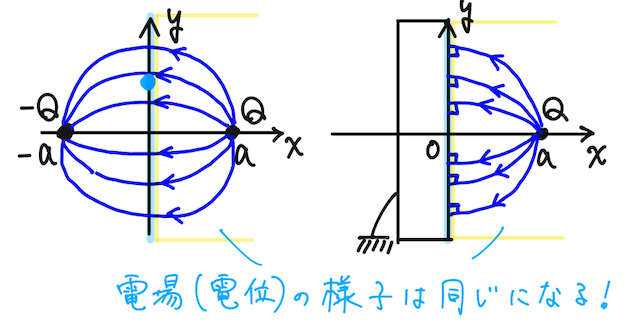
これは上で考えた、導体を置いていたときの状況とすごく似ていないだろうか。実は、冒頭に触れたポアソン方程式の解の一意性から、このように境界条件が同じであれば、電場の様子は一意に定まる。

つまり、導体が置いてあったときは、 の電場や電位の様子はよくわからなかったが、それを考えるときは、導体の代わりに に電荷 を置いて考えればいいことになる。これで高校物理でも電場や電位の様子を考えることができるようになった。