回折格子
概要
ガラスの片面に多くの細い筋を等間隔で平行に引いたものを、回折格子という。その筋同士の間隔
間違いやすいのが、その筋の部分は細かな凹凸によって、光を通すことができない(すりガラスのようなイメージ)。筋と筋の間がスリット(すき間) となり、多くのスリットを通り回折した光が干渉を起こし、スクリーンに明線が生じる。
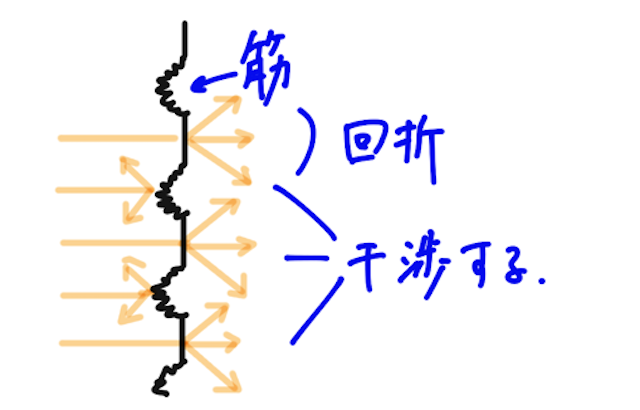
問題では、この干渉条件(強め合いの条件)がよく問われることになる。各スリットを通った単色光のうち、入射方向と
となる。ただし、
明線と聞くと、レーザーのような光線のイメージが浮かぶかもしれないが、明線とは、スクリーン上のその点が明るくなること。スリットは基本的に、平面上の直線のような形なので、スクリーン上では、そういう明るい点や暗い点が直線上に並ぶことになり、それを明線と呼んでいる。
なぜ他の干渉現象と違って暗線がないのだろうか? と思うかもしれないが、実は回折格子では多くの光が干渉することになるので、上の条件を満たす方向から少しでも外れると、位相が少しずれた各スリットからの光が重ね合わされ、全体として弱め合うことになる。
導出
干渉現象がたくさん出てきて潰れそうになるので、忘れても思い出せるようにしておこう。
こういう干渉の条件の導出はワンパターンなので、考え方を身につけてしまおう。
1. 光路差を考える
2. 位相のずれに注意する
3. 光路差が
今回は特に反射がないので、位相のずれは気にしなくて良い。まずは光路差を考える。
光路差
ここでは、スクリーンまでの距離
このとき、各スリットを通った単色光が、入射方向と
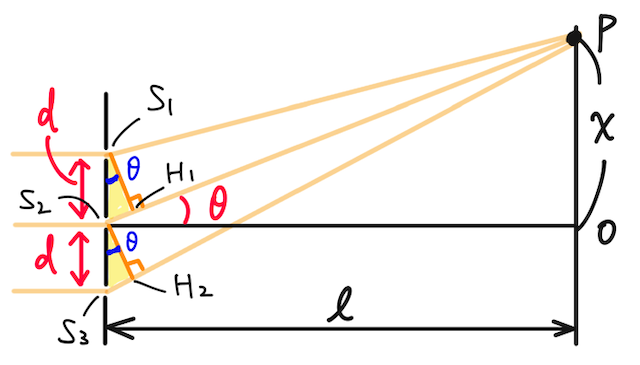
図のようなケースにおいて、まずは、スリット
このとき、スクリーンまでの距離が十分に長いとすると、
として良い。すると、光路差(光路長の差、今回は空気中で考えているので距離の差でOK)は、
と求められる。(
明線・暗線の条件
- 光路差が空気中(真空中)の波長
の整数倍であれば、重なった波はピタリと波形が一致するので、波は強め合い、明るく見える。つまり明線になる。 - 一方で、光路差が空気中(真空中)の波長
の整数 倍であれば、重なった波は完全に打ち消しあうので、波は弱め合い、暗く見える。つまり暗線になる。
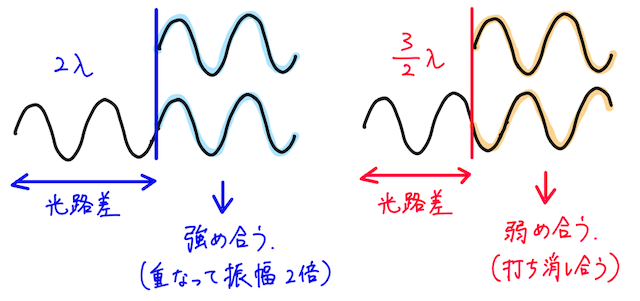
よって、回折格子の強め合い(明線)の条件は、
であることが示される。
補足
十分に
と近似することができる。

よって、光路差は、
と求められる。なので、明線の条件は、
でも表される。この形だと、スクリーン上の明線の間隔を求めやすく、
これらの隣り合う
と、スクリーン上の明線の間隔を求められる。これは ヤングの実験での明線の間隔と等しいが、ヤングの実験との違いは、回折格子では多くの光が強め合うので、より鋭く明線が現れる。
関連動画