合成容量

概要

回路に複数の抵抗がつながった問題で、直列接続や並列接続の場合に、合成抵抗を考えて解いたことがある方も多いと思う。物理的に1つの抵抗につなぎ変えるわけではなく、仮想的に1つの抵抗にまとめて、それが回路につながっていると考えて解くことができ、登場する抵抗の数が減ってとても便利な隠しワザだった。

実は、回路につながったコンデンサーを考えるときも、同じように合成容量というのを考えて、ラクができることができる。（コンデンサーの電気容量から来ているネーミング）

結論から言うと、電気容量 のコンデンサーを以下の形でつないだとき、1つにまとめたコンデンサーの合成容量 は次の式で求められる。合成抵抗のときと形が逆になることに注意しよう。

並列接続：

直列接続：

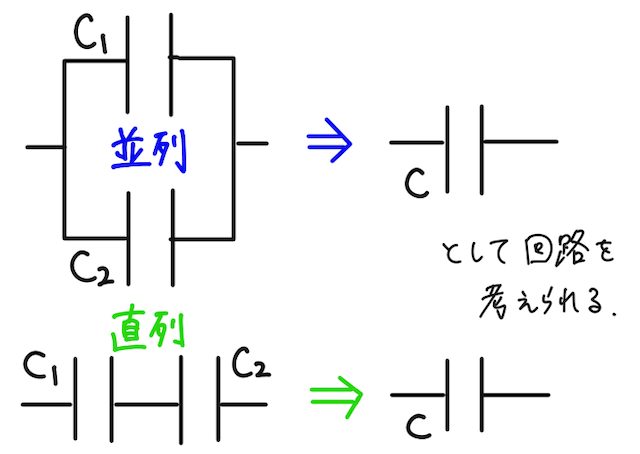
どっちがどっちかわからなくなるので、必ず下の証明も押さえておこう。

また、合成容量を使わないと解けない問題というのは無く、複雑な回路になったときに、変数を置いて地道に考える上での思考方法も、証明を通じて身につけることができるのでオススメ。

証明

大事なのは、

• 2つのコンデンサーでどの物理量が同じか
• どういう式で合成容量が求められるか

をしっかりと意識しておくこと。ここがわかっていると応用の幅が広がる。

並列回路

下の図のように、電圧 の電池に、電気容量 のコンデンサーが並列につながっていて、それぞれ電気量が 溜まっているとする。

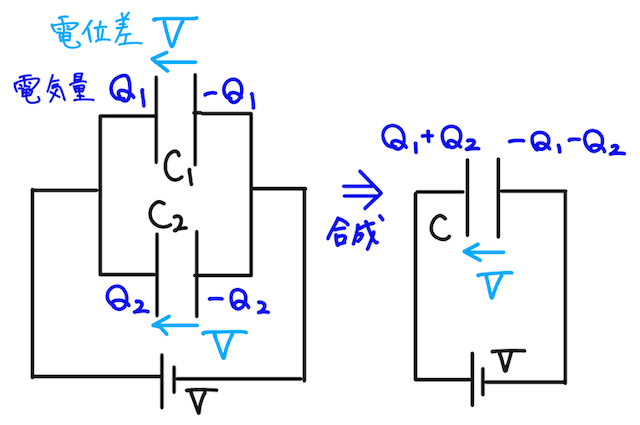
このとき、キルヒホッフの第二法則より、それぞれのコンデンサーでの電位差 は共通している。

そこで、それぞれのコンデンサーで電気容量の式を立てると、

となる。ここで、1つのコンデンサーに合成することを考えると、電気量は2つのコンデンサーの合計で となり、電位差はそのまま である。逆に言うと、このようなコンデンサーがあると考えれば、2つのコンデンサーを1つにまとめて、回路を考えることができる。

合成したコンデンサーの合成容量 は、電気容量の定義より、

と求められる。

直列回路

下の図のように、電圧 の電池に、電気容量 のコンデンサーが直列につながっていて、それぞれでの電位差を とする。

また、もともと電荷が溜まっていない場合には（後で補足）、電荷保存則より2つのコンデンサーの電気量は等しく、それぞれ電気量が 溜まっているとする。

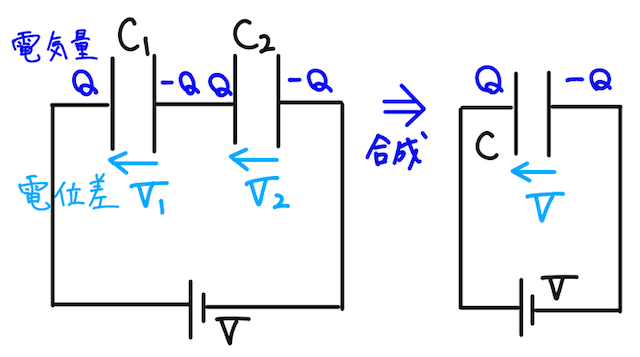
それぞれのコンデンサーで電気容量の式を立てると、

となる。さらに、キルヒホッフの第二法則より、

が成り立つ。

ここで、1つのコンデンサーに合成することを考えると、電気量は となり、電位差は である。逆に言うと、このようなコンデンサーがあると考えれば、2つのコンデンサーを1つにまとめて、回路を考えることができる。

合成したコンデンサーの合成容量 は、電気容量の定義より、

と求められる。

補足

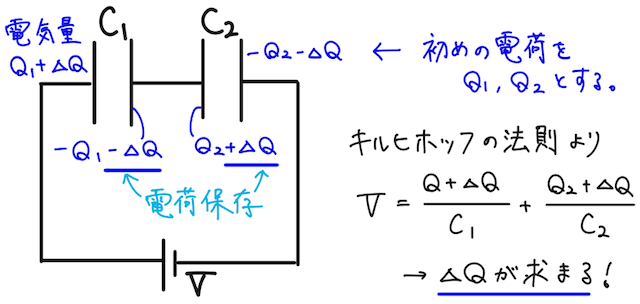
直列回路で、最初にコンデンサーに電荷が溜まっていたらどうするの？と思うかもしれない。その場合には、最初に溜まっている電荷によって合成したときの電気容量は変わってくるため、上の合成公式は使えない点に注意（ だけでは表せない）。

その場合は、コンデンサーを合成するという無理ゲーはせず、丁寧にキルヒホッフの法則を使って方程式を解いていくしかない。