ガウスの法則

概要

ある空間の電場の様子を目で見てわかるようにしたのが 電気力線 である。電場の強さが のところでは、電場に垂直な単位面積当たり、[本]の電気力線を描くことにするものであった。

そのようにして出てきた電気力線について、ここでは、電気量と電気力線の本数との関係を考える。

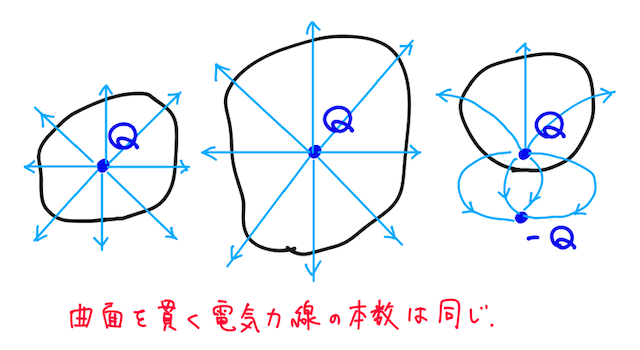
実は、任意の閉じた曲面（閉曲面）を取ってきたときに、その曲面から外向きに出ていく電気力線の合計本数 は、その曲面の内部に含まれる全電気量 のみによって決まり、

が成り立つ。これをガウスの法則という。

ただし、 はクーロンの法則の比例定数である。 は真空の誘電率といい、

で定義される。

また、 が負のときにも成り立ち、 が負というのは、電気力線が内向きに入っていくことを意味する。

ガウスの法則のすごいところは、閉曲面をガサッと適当にとったときに、その中で電荷がどのように分布していても、閉曲面から出る電気力線の合計本数が上の式で求められてしまうということ。そのときに、曲面内の全電気量が一緒であれば、電気力線の合計本数は同じになる。（もちろん曲面上の各点での電場の強さは違ってくるが、曲面上の全てを合計すれば一緒になるようなイメージ）

点電荷を中心とした球面

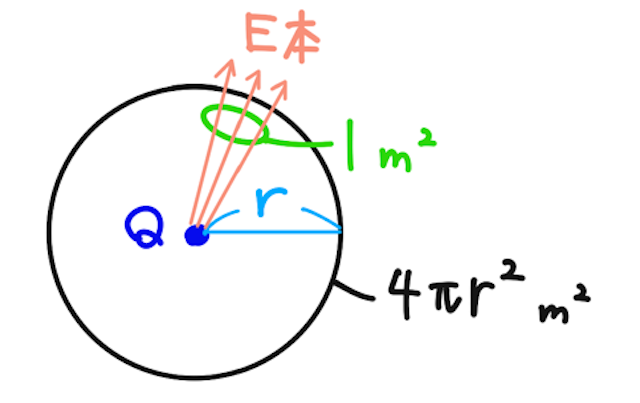
ここでは、真空中に点電荷 をおき、それを中心とした半径 の球面を考えて、上のガウスの法則を納得しよう。（それ以上の証明は大学のお楽しみ）

点電荷が球面上に作る電場は、

で一定になるので、この球面上では単位面積（）あたり 本の電気力線が貫くことになる。

よって、閉曲面（球面）全体から出ていく電気力線の合計本数は、球の表面積をかけて、

となることが示される。