自己誘導

概要

電磁気の最後の方に出てくるので既読スルーされがちな自己誘導だが、「なぜそんな現象が起こるのか」「どうやって公式が出てくるのか」がわかれば怖くないし忘れなくなる。

まず、電磁誘導によって生じる誘導起電力の向きや大きさ、と聞いてピンと来ない方は、先にレンツの法則やファラデーの電磁誘導の法則を確認しよう。

コイルを含んだ回路を考えて、コイルに流れる電流が時間によって変化するとする。このとき、電流によって作られる磁場の強さも変化し、コイルを貫く磁束が時間によって変化することになる。

よって、電磁誘導が生じ、その変化を打ち消す方向にコイルに誘導起電力が生じる。この現象を自己誘導という。

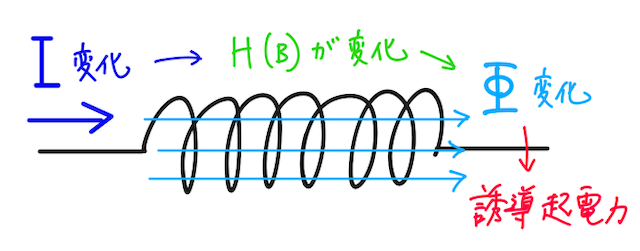
これを式で表してみよう。

まず、電流がコイルの内部に作る磁場 の強さは電流 に比例する。そして、磁束密度 は磁場 に透磁率をかけたものであり、磁場 に比例する。さらに、磁束 は磁束密度 に比例する。

よってまとめると、コイル内の磁束 は電流 に比例する。（これまでの知識のいい復習にもなるので、それぞれの辞書で定義などを復習しておこう）

そこで、この比例係数を とおくと、

と表せる。

これより、時間 の間に電流が 変化するとき、磁束の変化 は、

と表せる。よって、巻き数 のコイルに生じる誘導起電力 は、ファラデーの電磁誘導の法則より、

を得る。ここで、比例係数をまとめて とおくと、

と表せる。この、自己誘導によって生じた起電力を、そのままのネーミングで自己誘導起電力といい、この比例係数 のことを、自己インダクタンスと呼び、自己誘導の大きさを表す。単位はヘンリー を用いる。

この式は符号付きになっていて、電流の正の向きに、電流を流そうとする起電力を正として考える。なので上の自己誘導起電力の式は、コイルの自己誘導では、電流の負の向きに電流を流す起電力がはたらくことを意味している。

このように定められる誘導起電力の向きは、もちろんレンツの法則により定まる向きとも一致している。つまり、レンツの法則によると、磁場の変化を打ち消す方向に誘導起電力がはたらくが、それはつまり電流の変化を打ち消す方向であり、上で考えた向きと同じになる。