点と直線の距離

概要

直線 と点 の距離は

で計算できる 。「距離」とはつまり点から直線に下ろした垂線の長さで、図のイメージは以下の通り。

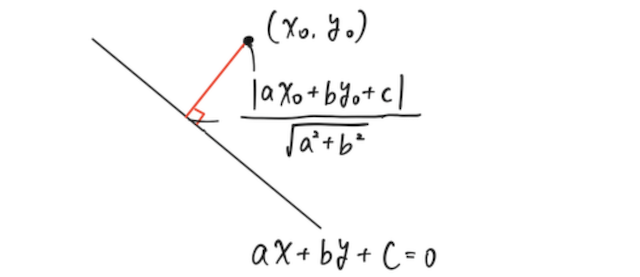
絶対値が出てくるので、高校生から嫌われる傾向にあるが、円と直線の位置関係 を調べるときなど、大学入試において頻繁に使う公式の一つになるので、使い方だけでも確実に押さえておこう。

例

点 から直線 までの距離を求める。直線の式を変形すると、

なので、距離は、

と求められる。

証明

図形的に示すあらすじとしては、以下の通り（都合上、 は ではないとする）。この他にも様々な証明がある。例えば、もっと簡潔にベクトルで示す方法があるので、ガチでノビる受験数学さんの動画やMathkaratさんの動画を参照。

点 と直線 との距離を求める。

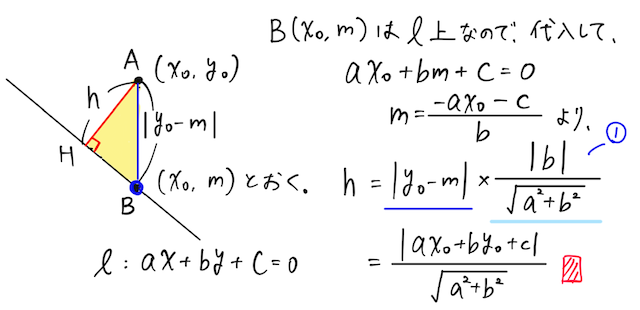
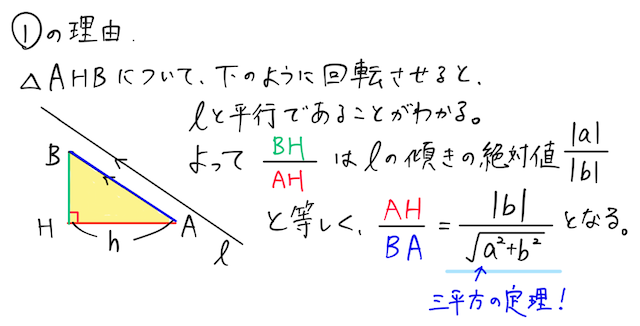
図形で示すと、上下関係や正負がわからないので、このように絶対値で話を進める必要がある。

補足

• 2013年に大阪大学の入試問題で出題されたことでも有名
• 慣れるまでは、必ず直線の式を の形に直してから使うようにしよう
• 絶対値を付けるのを忘れがちなので、注意
• 分子は、直線の式の に点の座標を代入して絶対値、分母は三平方の定理っぽい形と覚えておくと、思い出しやすい
• 証明の都合上、 は ではないとしたが、 になる場合は、直線は 軸に平行になるので、 座標の差で直線までの距離を求められる。結果として、上の形と同じになる（ も になると直線の式を表さないので、）