中間値の定理

概要

難しく書くと、 が閉区間 上で連続ならば、 と の間の任意の に対して、 を満たす実数 が、 に存在するという定理を、中間値の定理という。

日本語だと発狂しそうな人は、 図でイメージを確認すると、 意外と簡単なことを言っていることがわかるはず。

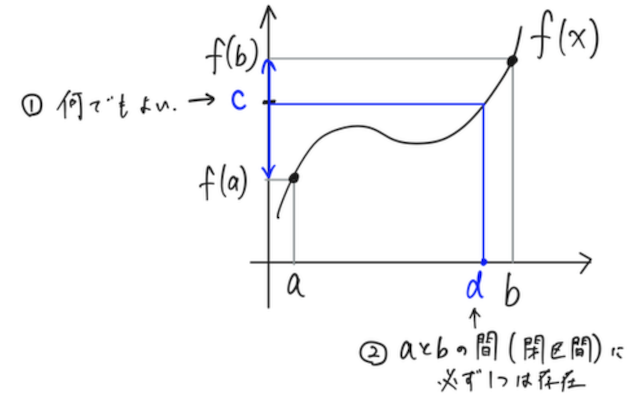
①なんでもいいから、 と の間の値 を取ってくると、

②それに対応した が、 に存在する。

例

【問】方程式

が、区間 で解をもつか調べよ。

【答】(左辺) とおくと、 は連続であり、 かつ である。

よって、中間値の定理から、 を満たす が閉区間 に少なくとも一つ存在するので、解を持つ。（閉区間は、両端も含まれる区間のこと）

このように、グラフの形状がわからなくても、 両端の情報だけで、解があるかどうかを調べられるのが、この定理の便利なところ。

補足

色々な前提（閉区間、連続など）がついているが、どれも欠かすことはできない重要なチェックポイントなので、答案で使う場合はしっかりと前提を確認しよう（高校の範囲だと基本的に成り立っているけどね）。

平均値の定理とややこしいが、こちらは と の「中間」を取ってきているというイメージ。（平均値の定理の辞書はこちらから確認）