関数の連続性

概要

関数がある で連続というのは、直感的にはそこでグラフが途切れずにつながっているということ。

それをカッコよく数学的に表現すると、以下のような定義になる。

「関数 が定義域内の で「連続」とは、 が存在し、その値が に等しいこと」

ポイントは下の通り3つあり、 全てをクリアしないといけない。

• が定義されていて
• と が一致して
• その極限値と が等しくなる

2つ目はつまり、 を の右から近づけた右側極限と、 を の左から近づけた左側極限についての一致で、つまり極限値 が存在するということを確認している。

（もしその点の両側で分ける必要がなさそうであれば、一気に極限を出しても良い）

吐き気がした人もしていない人も、下の図と例で確認しよう。

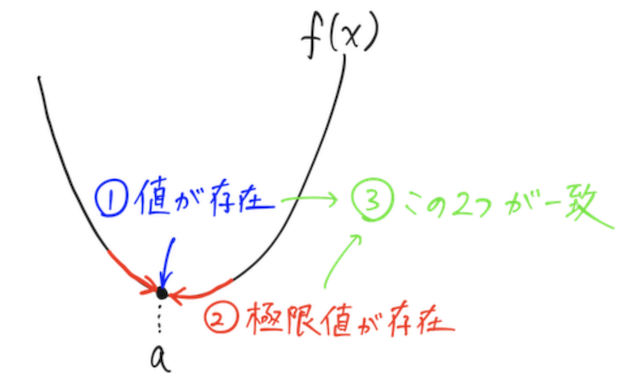
定義域内のある点について、上のポイントがどれか欠けると、関数 はそこの点では不連続であるという。

例

は で連続か？

① は定義されているので、存在する（値は ）。

② の左右で関数の様子が変わるので、右側極限と左側極限に分けて考える。

右側極限は、

（ の右側極限を考えているので、。よって が得られる）

左側極限は、

（ の左側極限を考えているので、。よって が得られる）

となり、左側極限と右側極限は一致して、極限値 をとる。

③ ②で一致した極限値と①で確認した の値は一致するので、 は で連続。

証明

• ある区間のどこの点でも連続であれば、関数 はその区間で連続と言える。
• いちいちここまで詳しく証明しなくても、連続であることが当たり前のときは、証明なしで「連続なので」と書いてOK。
• ある関数が微分可能ならば連続である。逆は成り立たない。（微分可能性については、こちらの辞書で確認）