概要
三辺の長さが の三角形が存在するための必要十分条件は、
が成り立つことである( は「かつ」の意味)。これを三角形の成立条件という。またの名を三角不等式ともいう。どれかを満たしていなければ、三角形が潰れるなどして成立しない。
もう少しきれいな形を目指してみよう。それぞれの不等式を について整理すると、
となる。ここで、最後の 本は
とまとめられるので、結局
とスッキリ つの式にまとめることができる。これも三角形の成立条件であり、三角不等式である。
についてしかまとめてなくない?と思うかもしれないが、この つの式で最初の つの不等式と同値なので、これだけ考えとけばOK(もちろん真ん中の項を や について整理しても同じ)。 本で考えられるので、とても便利な式。ただ、最初の つの三位一体型の不等式の方が、対称的で形が綺麗という説もある。
例
【問】三辺の長さが である三角形が存在するような の範囲を求めよ。
【答】題意の条件が成り立つための の必要十分条件は、
と求められる。
※ここでは、 が主役なので、真ん中を にした方が圧倒的に楽!ただ、もちろん や を真ん中に持ってきても同じ結論になる。
補足
ある三角形があったときに、余弦定理を使ってこの条件を導いてみよう。
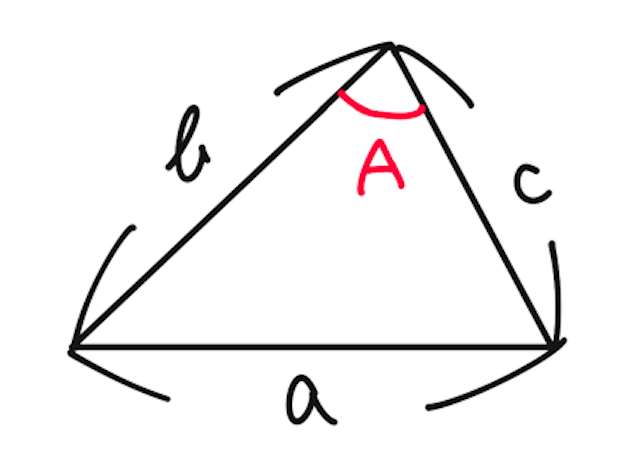
上の三角形を考えると、余弦定理より、
ここで、三角形が成立しているとき、 より なので、
となって、三角不等式が出てくる。最後の式変形は、全ての辺が 以上であるため可能。
逆の証明、つまり「三角不等式が成立する 三角形が成立する」、についても、もし興味があれば考えてみよう。
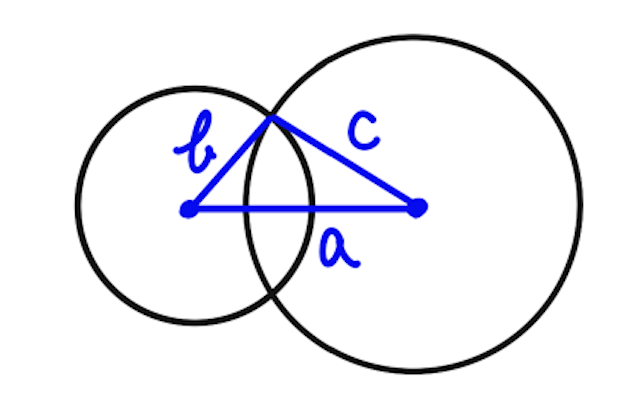
あらすじとしては、半径が の つの円を考えて、中心間の距離を にすると、三角不等式と 円の位置関係から、 つの中心と交点を頂点に持つ三角形を作ることができる。