平均値の定理

概要

堅苦しく書くと、 が閉区間 上で連続、開区間 上で微分可能ならば、

を満たす が、 に存在するという定理を、 平均値の定理という。

日本語だと気が狂いそうな人は、図でイメージを確認すると、 意外と簡単なことを言っていることがわかるはず。

と を結んだ傾き、つまり と、接線の傾き が等しくなるような点が、 に存在する（このグラフだと 個ありそう）。

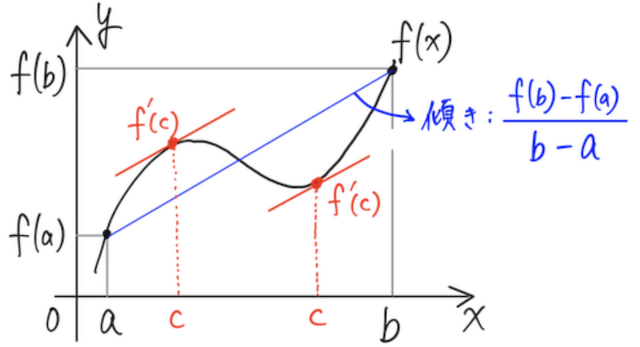
例

不等式を証明する問題が、よく問われる。このとき、 は自分で見つけてこないといけない場合が多い。

例えば、 のもとで、

を示す。

関数 とおくと、この関数は で連続かつ微分可能なので、平均値の定理を用いることができて、

を満たす が、 に存在する。

いま、 なので、。よって、 が成り立つので、

が示される（ より なので、不等号の向きは変わらない）。

このように、具体的な の値は最後までわからなくても、不等式が証明できてしまうのが、平均値の定理のすごみ。

補足

分母を払った、

という形もよく使う。

色々な前提（閉区間、開区間、連続、微分可能など）がついているが、どれも欠かすことはできない重要なチェックポイントなので、答案で使う場合はしっかりと前提を確認しよう（高校の範囲だと基本的に成り立ってはいる。各前提が必要な理由は下で解説）。

中間値の定理とややこしいが、こちらは と の「平均」の傾きを取ってきているというイメージ。

証明については、教科書には書かれていないことが多いので、こちらのヨビノリさんの動画を参照しよう（1本前のロルの定理の証明から見ることをオススメする）。こちらの古賀真輝さんの動画もオススメ。

連続性や微分可能性が必要な理由

グラフで理解しておこう。まず、平均値の定理が成り立つ上で、閉区間 上で連続であることが必要な理由は、以下のような場合があるため。

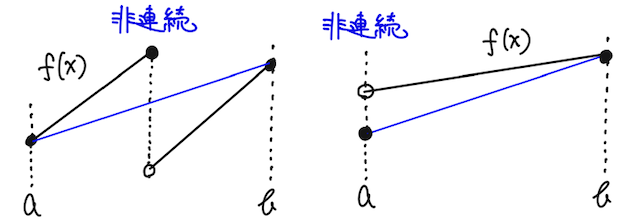
このとき確かに、 と を結んだ青い線の傾きと、接線の傾き が等しくなるような点は、 に存在しなくなる。

また、平均値の定理が成り立つ上で、開区間 上で微分可能であることが必要な理由は、以下のような場合があるため。

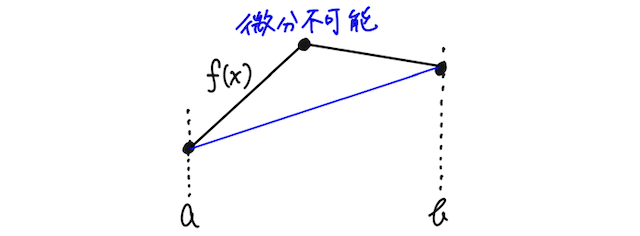
このときも確かに、 と を結んだ青い線の傾きと、接線の傾き が等しくなるような点は、 に存在しなくなる。