薄膜による干渉

概要

水面に、油などの薄い膜（薄膜）が広がっているとする。このとき、空気と薄膜の境界で反射した光と、薄膜と水の境界で反射した光が、干渉して色づいて見えることがある。この現象を、薄膜による干渉という。

ここでは水面上でとりあえず考えるが、実は空気によってはさまれた薄膜でも干渉が起こり、これがまさに、シャボン玉が、見る角度によって色々な色に見えるカラクリである。「薄膜」ってどんくらい薄いのか気になって、これまで夜しか眠れなかった人もいるかと思うが、思ったより薄いなとわかると思う。

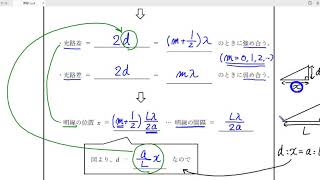
まずは、干渉が起こる条件について、結論を示そう。下の図のように、厚さ 、(絶対)屈折率 の油などの媒質が水面に広がっているとし、 は水の(絶対)屈折率よりも大きいとする。

その膜へ、波長 の光（決まった波長なので単色光）が入射角 で入射したとし、ある点で屈折角 で屈折し、水との境界で反射して、また屈折して空気中に出てきた屈折波（水色）と、その点で反射した反射波（オレンジ）との干渉を考える。

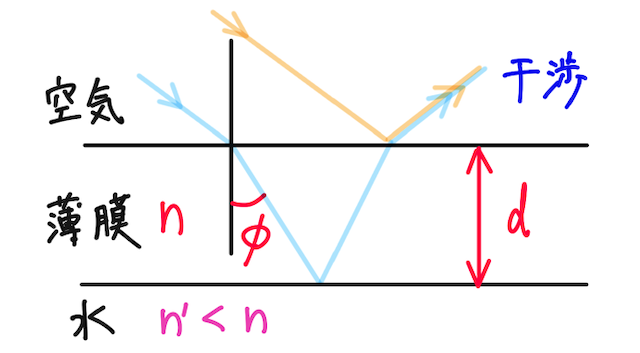
このとき、その光の干渉条件は、 として、

となる。明線・暗線と聞くと、レーザーのようなイメージが浮かぶかもしれないが、明線とは、薄膜上のその点が明るく見えること。逆に、暗線とは、薄膜上のその点が暗く見えること。膜として平面で見たときに、そういう点が薄膜上に直線上に並ぶので、明線・暗線と呼んでいる。

導出

こういう干渉の条件の導出はワンパターンなので、考え方を身につけてしまおう。

1. 光路差を考える

2. 位相のずれに注意する

3. 光路差が の整数倍か、整数 倍かで強め合い・弱め合いを判断する

光路差

この場合の光路差は、折れ線を伸ばすとわかりやすい。

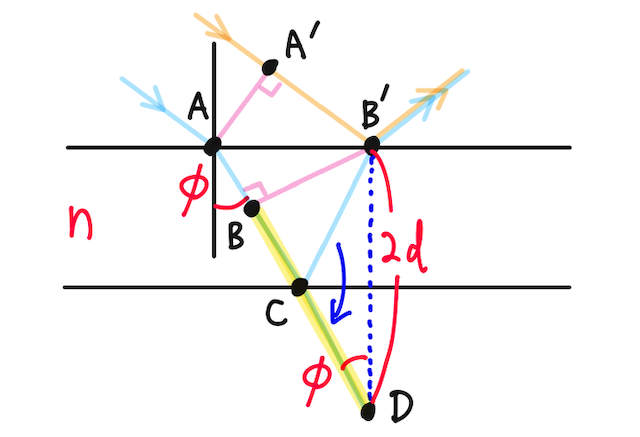
まずは経路差を求める。 は波面になり、水色の波とオレンジの波は、同時刻にそれぞれ と にいる。その後、オレンジの波が点 に到達するとき、水色の波は点 にいる。（ここがわかりにくい方は、ホイヘンスの原理および屈折の法則の導出を復習しよう）

オレンジの波はそこから反射し、水色の波は と進むので、経路差は

となる。点 を図のように折り返した点を とおくと、

となるので、経路差は の長さということになる。（これを と勘違いしてしまいがちなので、上の流れをしっかり押さえよう！）

錯角より 、折り返したので なので、 に着目すれば、

を得る。（もうちょっとでゴール！）

今、経路差を求めたが、空気中の波長 で話をするため、ここでは光路差を考える。補足で述べるように、ここを経路差のまま考えて、薄膜中での波長で計算する方法もある。

薄膜の(絶対)屈折率は なので、光路差は、

となる。

位相のずれ

干渉の問題で大事な事実として、

• 絶対屈折率が小さい媒質から、大きい媒質に入射する波が反射すると、位相が ずれる。
• 絶対屈折率が小さい媒質から、大きい媒質に入射する波が反射すると、位相はずれない。

正弦波の式を思い出すと分かる通り、位相が ずれるとは、中身の角度が ずれること。例えば、山で入射した波は谷として反射する。

この証明は大学になってから学ぶ事になるが、固定端・自由端と同じイメージで、硬そうなものにバンっとぶつかって反射するときには ずれて、柔らかそうなものにフニャっとぶつかって反射するときには位相はずれない、という理解をしておこう。

なお、ややこしいが屈折波については、媒質の屈折率によらず位相は変化しない！

では、この薄膜の問題では、どこで位相がずれるだろうか。

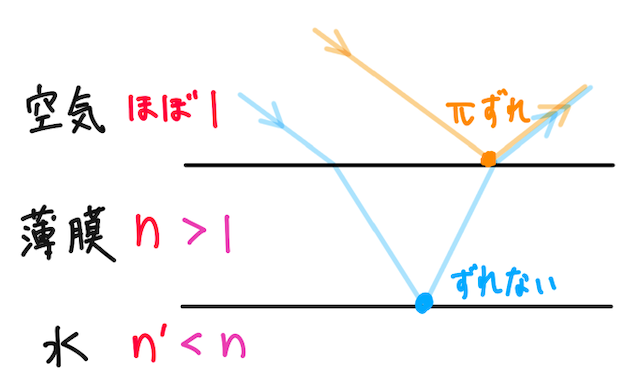
上の図の赤の文字が、それぞれの媒質の絶対屈折率を表す。これより、オレンジの波は、反射する際に位相が ずれるが、水色の波は、位相がずれるタイミングはない。

明線・暗線の条件

つの波に位相のずれがない場合は、

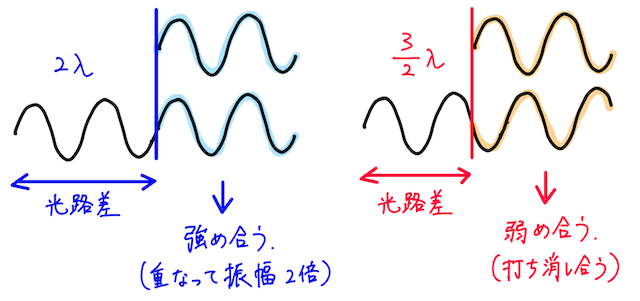
• 光路差が空気中（真空中）の波長 の整数倍であれば、重なった波はピタリと波形が一致するので、波は強め合い、明るく見える。つまり明線になる。
• 一方で、光路差が空気中（真空中）の波長 の整数 倍であれば、重なった波は完全に打ち消しあうので、波は弱め合い、暗く見える。つまり暗線になる。

※ この波の色は、今回の問題の波の色とは関係ありません...

一方で、どこかで位相の のずれが起こっている場合には注意が必要で、強め合い、弱め合いの条件が逆になる可能性がある。今回の薄膜による干渉では、オレンジの波だけ反射の際に ずれているので、

• 光路差が空気中（真空中）の波長 の整数倍のとき、位相のずれを考えると、重なった波は完全に打ち消しあうので、波は弱め合い、暗く見える。つまり暗線になる。
• 一方で、光路差が空気中（真空中）の波長 の整数 倍のとき、位相のずれも考えて、重なった波はピタリと波形が一致するので、波は強め合い、明るく見える。つまり明線になる。

よって、干渉の条件（明線・暗線の条件）は、 として、

であることが示される。

※位相のずれが片方に 回起こったり、どっちの波もずれていたりすると、効果を打ち消し合うので、位相のずれがない場合と同じ結論になる。

補足

ここでは説明上、空気・薄膜・水の三段腹で考えたが、導出を確認すれば、何でも良いので三層構造になっていれば干渉が起こりうる（ただし屈折率の条件によって、暗線・明線の条件は異なる）んだと分かるし、それが応用力につながっていく。

厚膜じゃダメなの？ と思う方もいるかもしれない。実は が大きくなると、その分干渉条件から も大きくなるが、 と の比が近づいていくので、波長が少しゆらぐと明線・暗線の条件が安定しないので、厳しい。

また導出において、経路差のまま考えても結論は変わらない。経路差は上で見た通り、 であり、薄膜中での波長は、屈折の法則より なので、干渉条件は、

となり、両辺に をかければ、上の干渉条件と一致することがわかる。

あと、難しい問題になると、薄膜内でピンボールみたいに何回も反射しながら干渉したりするが、その際にも上の考え方で考えていけるので、とにかくこのテーマは考え方を正しく理解しよう！