概要
「ファンデルワールスの状態方程式」とは、理想気体の状態方程式の実在気体バージョンのこと(*注1)。実在気体では分子体積・分子間力が無視できない分、気体の種類によって決まる定数、が必要になり、以下のように表せます。
によって分子間力の影響を、によって分子体積の影響を表していて、それぞれの影響をとすれば理想気体の状態方程式となります。
ちなみに大学入試的には原則覚える必要も理解する必要もありませんが、問題文での説明付きで出題される可能性はあります。
詳細
理想気体では分子間力と分子体積を無視しますが、実在気体ではそれぞれの影響が出てきます。
分子間力の影響
実在気体の圧力とは、容器の外から測定したときの圧力です。しかし実は、分子間力がなければ(=理想気体なら)出せたであろう圧力よりも小さくなってしまっています(はideal gasの頭文字)。なぜなら、分子が壁にぶつかって圧力を及ぼすときに、分子間力によって引き止められるからです。
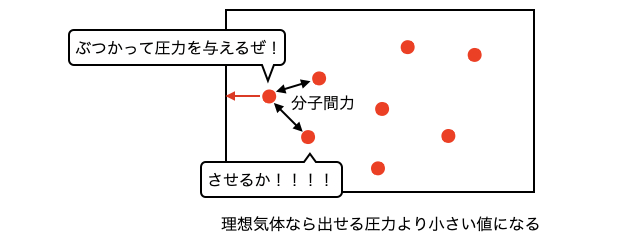
周りの分子が多いほど強く引き止められるので、1分子を引き止める力は濃度に比例します。そして温度一定なら圧力は濃度に比例する、つまりぶつかる分子の数と圧力が比例します。以上を合わせれば圧力の減り具合はに比例します。
よって比例定数をとすれば、
と表せそうです。
分子体積の影響
実在気体の体積とは、容器の容積のことです。しかし、分子に体積があると分子が多いほど混雑してしまい、実際に動ける空間が減ってしまいます。つまり体積、「実際に動ける空間」を意味する理想気体の体積よりも分子体積の分だけ体積を過大評価してしまっています。
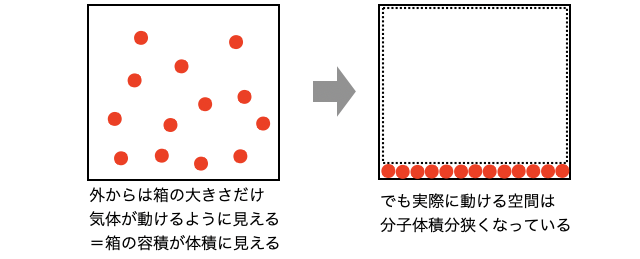
分子体積の影響は単純に気体分子の数に比例して大きくなるので、比例定数をとすれば、
と表せそうです。
実在気体の状態方程式の導出
圧力、体積の理想気体であればが成立しそうです。これまでの結果を、について整理すると、
これをに代入することで、ファンデルワールスの状態方程式が得られます。
補足
- (*注1)ファンデルワールスの状態方程式は、あくまで実在気体を考えるためのモデルの1つです。つまり 「分子体積と分子間力の影響をそれっぽく考えるとこの方程式になり、しかもそれが実験結果に近いから便利だよねー」、という式です。100%実在気体を表現したものではありませんが、実用上便利なのでよく使われます。