階級区分図

階級区分図

分布図は特に説明しなくとも直感的に分かるものが多いのですが、階級区分図だけは取扱注意なのでまるまる一項目使って説明しようと思います。

階級区分図は、階級ごとに色分けして塗り分けた地図のことです。地域は、国境や県・州・省などの行政区分で分けられることが多いです。よく見かけますよね。

視覚的に非常に分かりやすく、訴求力が高いためよく用いられるのですが、誤解も招きやすいため、意図を正しく伝えるためにさまざまな決まりがあります。しっかり覚えましょう。

階級の区切り方

階級は、適切に割り振らないと階級を分けた意味が無くなります。例えば、

• ０～２５％
• ２６～５０％
• ５１～７５％
• ７６～１００％

のように均等に区切っていけばいいのですが、

• ０～１０％
• １１～９０％
• ９１～１００％

みたいなことをすると意味がなくなってしまいます。ほとんどが１１～９０％の階級に属してしまい、同じ色の中でも本来あるはずの差異がわからなくなってしまいます。

色の塗り分けは段階的に

色の塗り分けは、「少ない場所は薄く、多い場所は濃く」を基本に、分かりやすく塗り分けなければなりません。用途に応じて様々な塗り分け方がありますが、基本的にはこんな感じの塗り分けが理想です。

一方で、分かりにくい塗り分けもあります。

このような塗り分けだと、赤が少ないのか、青が少ないのか、緑が少ないのか、よくわかりません。混乱を招かないようにも、連続した色を用いるようにしましょう。

相対分布図のみに用いる

一番重要な鉄則です。決して、絶対分布図を階級区分図で表してはいけません。

これにはちゃんと理由があります。下の図をご覧ください。左側が、誤った地図です。

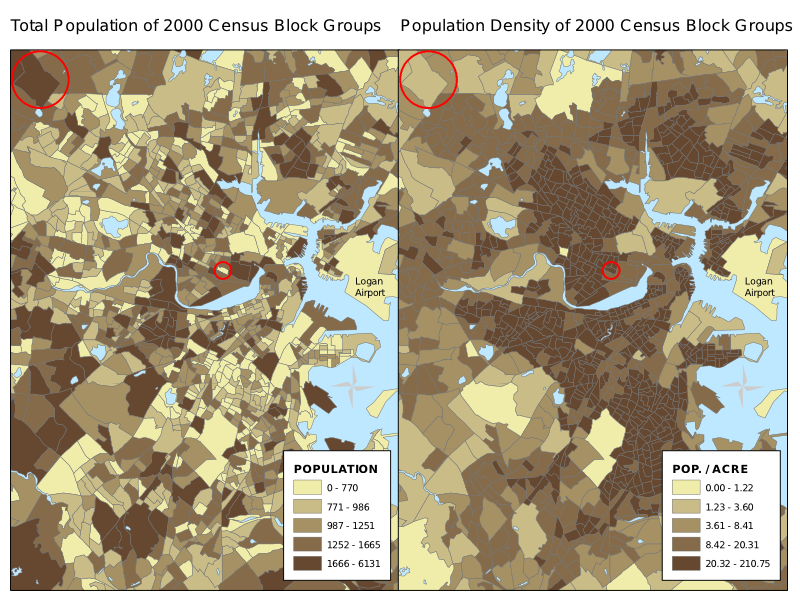
この図はボストンの地図で、左が人口、右が人口密度を表しています。つまり左が絶対的な値、右が相対的な値です。

この小さい◯がついているあたりが中心市街地で、大きい◯がついているあたりが郊外なのですが…

普通に考えて、中心部の方が人口が密集していて、郊外の方がまばらなはずですよね。でも、左の図ではそれが全く伝わってきません。むしろ、郊外の方が人口が多いように見えてしまいます。一方で、右の図は実態をよく表していますよね。

なぜこのような事態が起きるのか、これにはちゃんとした理由があります。その理由は、

• 人口分布には偏りがある
• 地域区分ごとの面積が均等ではない

この二点です。

人口分布は均一ではありません。必ず偏りがあります。

このような状態で、絶対数を用いた階級区分図を正しく表現しようと思ったら、均等な面積で区切らなければなりません。面積を均等に分けられれば、人口分布の偏りをそのまま反映させることができるからです。

しかし、県や市などの行政区分では、面積は均等にはなりません。面積を均等に区切らなければ、何が起こるでしょうか。ちょっと実験してみましょう。

人口が西部に偏った国を想定してみます。西側は人口密集地ですが東側はまばらです。どこかの国みたいだと思った人、思っても口に出してはいけません。

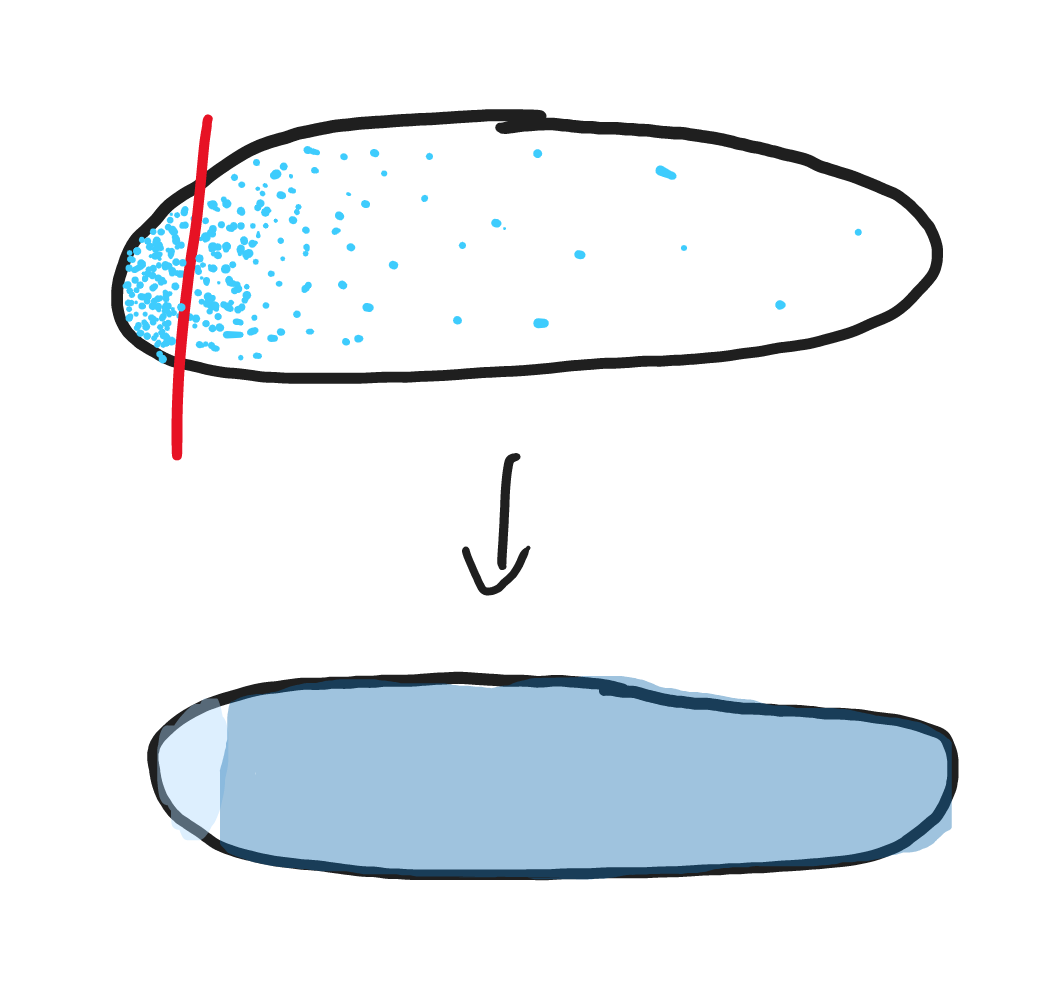
面積を不均等にするために、めっちゃ左側で切ってみましょう。

こうすると、さすがに人口の絶対数でいえば右側の方が多くなります。人口の絶対数に応じて塗り分けると、右側の方が濃い色になりますよね。

この地図だけ見ると、右側の方が人口多そうに見えませんか？ いや、実際に人口は多いんですが、右側の方が人がたくさんいて発展した地域なんじゃないかと、誤解してしまわないでしょうか？ 実際に発展している地域は左側なのに。

なぜこういう勘違いが起こるのかと言えば、人間は絶対数と密度を分けて考えることは直観的にはできず、同じ色の区域内は均一な状態であると考えてしまうからです。

上の図でいえば、色の濃さは単に人口の合計を表しているだけなのに、直観的には人がたくさんいそう、この広い領域全体にまんべんなく多くの人がいるのだろう、と直感的に考えてしまうのです。

また、もとのデータを知っていれば直感的な誤解で済み、あとからいやこれは違うと考え直せますが、元を知らなければこれは分かりようがありません。本当に右の方が発展しているのかもしれない、はたまた今回のような状態なのかもしれない、どちらかは絶対に分かりません。これでは分布図としては不適切です。

では、これを解決するにはどうすればよいか。はじめに挙げた原因を潰せばよいのです。

原因は、

• 人口分布には偏りがある
• 地域区分ごとの面積が均等ではない

でした。ですから、

• 面積当たりの人口で比較
• 均等な面積で比べる・・・メッシュマップを利用

という対策が考えられます。

単位面積当たりの人口（＝人口密度）で比べれば、区域の面積の広さは一切関係なく比較できます。また、メッシュマップのようにすべての区分を均等な面積にすれば、人口の偏りをそのまま反映させることができるので、絶対数でも問題なく表現できます。