力のモーメント

概要

物体に力を加えても変形しない理想的な大きさのある物体を考えて、これを剛体という。どんなに複雑な剛体であっても、運動は次の2種類に分けられる。

• 並進運動（向きを変えずに平行に移動する）
• 回転運動（ある点の周りの回転）

大きさを考えない質点のときは、回転運動は考えてなかったが、剛体だと回転運動が登場する。

回転運動を考える上で、剛体に力がはたらいているとき、どれくらい剛体を回転させようとするかを表すものが欲しくなる。

そこで出てくるのが力のモーメントで、剛体にはたらく力の大きさ と、ある点からこの力の作用線までの距離 （これをうでの長さという）の積として定義される。

この定義から、単位はニュートンメートル であることがわかる。

この定義は、なんとなくイメージでも理解できる。力が大きい方が剛体を回転させるはたらきが大きくなるし、距離が大きい方が剛体を回転させるはたらきが大きくなる。

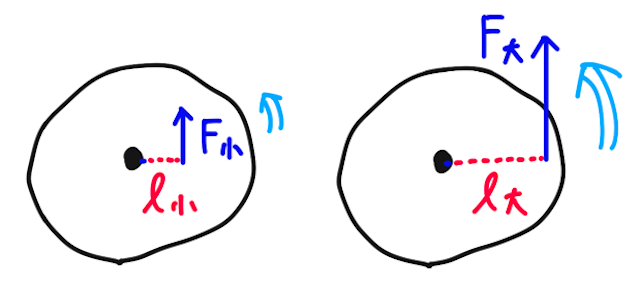
詳しくは剛体のつり合いの辞書で学ぶが、剛体が回転しないための条件は、合力が であって、任意の点のまわりの力のモーメントが0になることである。

例

【問】下の図のように、軽い棒に3つの力がはたらいているとする。

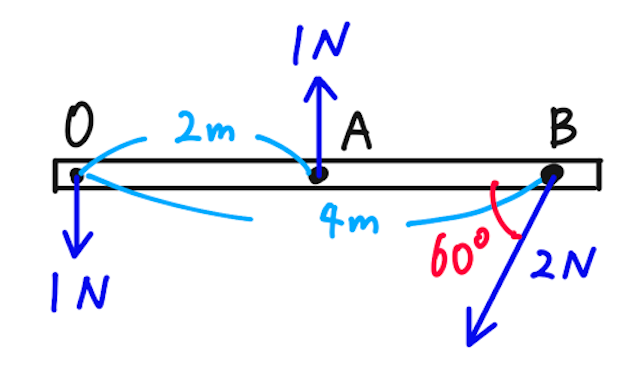
（1）点Bのまわりの力のモーメントの和を求めよ。反時計回りを正とする。

（2）点Oのまわりの力のモーメントの和を求めよ。反時計回りを正とする。

【答】

（1）点Oにはたらく力は、反時計回りに棒を回そうとするので、力のモーメントは、

点Aにはたらく力は時計回りに棒を回そうとするので、力のモーメントは、

よって、点Bのまわりの力のモーメントの和は

となる。

（2）点Aにはたらく力は、反時計回りに棒を回そうとするので、力のモーメントは、

点Bにはたらく力は時計回りに棒を回そうとする。さらに、うでの長さは、

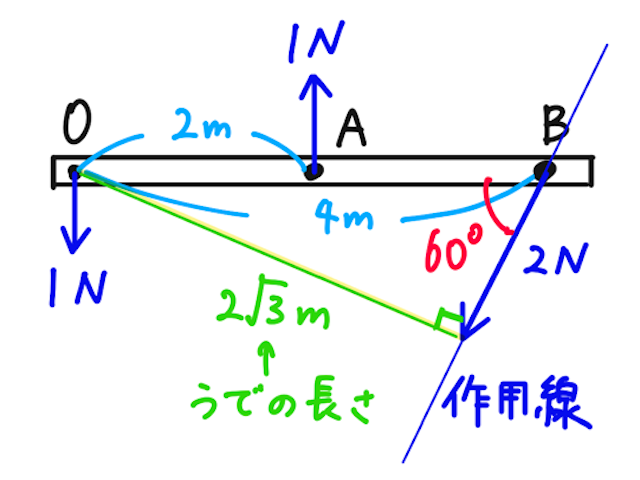
となるので、力のモーメントは、

よって、点Bのまわりの力のモーメントの和は

となる。

補足

モーメントの求め方は、上の通り、力の大きさ×うでの長さで考えてもいいが、力を成分に分けてしまってもいい。

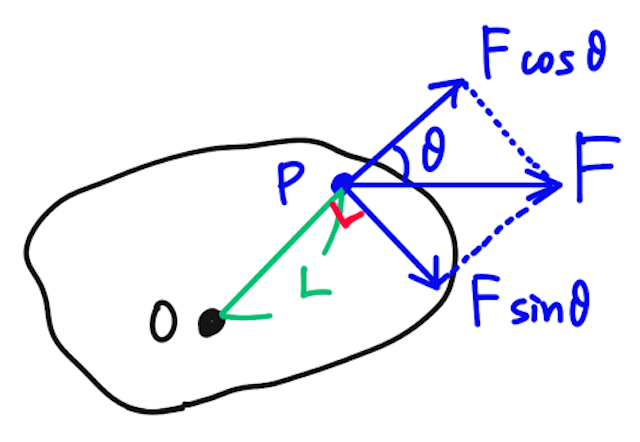
このとき、OPの方向の成分は、物体を回すはたらきをしないので、モーメントは0となる。OPを垂直な方向の成分の力のモーメントだけ考えればよく、

となる。力の大きさ×うでの長さ、で考えると、

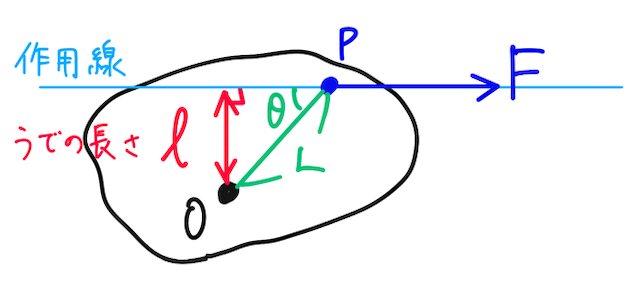
となるので、確かに一致する。考えやすい方を考えればOK。