コイルのエネルギー

概要

コイルの自己誘導によって生じる誘導起電力に逆らってコイルに電流を流すとき、電荷が高電位から低電位へと移動するので、静電気力による位置エネルギーを失う。この失った位置エネルギーは電流のする仕事となり、全てコイル内にエネルギーとして蓄えられる。この式を求めてみよう。

ちょっと思い出してみると、抵抗を含む回路では、電流が抵抗を流れるときに、電荷が静電気力による位置エネルギーを失い（失った分を電力量と呼んだ）、全てジュール熱として放出されたのであった。コイルの場合はそれがエネルギーとして蓄えられるというだけの話。

コイルの自己インダクタンスを とし、コイルに流れる電流を とすると、コイルの蓄えるエネルギー は

で表される。

たまに 「磁場（磁界）のエネルギー」 とも呼ばれるので合わせて押さえておこう。

導出

自己インダクタンス のコイルに、電流を から になるまで流したときの、コイルのエネルギーを求める。

微小時間 の間に、電流が から に変化したとする。このときコイルに生じる自己誘導起電力の大きさ は、

であり、電流とは逆向きに生じる。

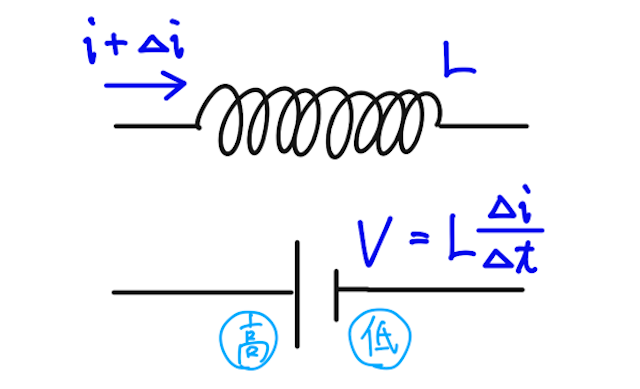
電流はこの自己誘導起電力に逆らって流れており、微小時間 の間にコイルを流れる電荷を とすると、

と表される（ は限りなく微小なので、電流は で一定と見なせると考えよう。あとで微積でも見てみる）。

この電荷が失う静電気力による位置エネルギー（これがつまり電流がする仕事になる） は、電位の定義より、

となる。（電力量でも学んだ考え方）

変形すると、

ここで を限りなく小さくしていくと、

となるので、両辺を から まで積分すると、

と求められる。これがつまり電流がする仕事になり、コイルが蓄えるエネルギーになるので、

となる。

補足

コンデンサーの静電エネルギーの形と似ているので、整理しておこう。

• コンデンサーの静電エネルギー：
• コイルのエネルギー：

また、上では を駆使して導出したが、微積を少し使うとこんな感じになる。（マニアックなので、読み飛ばそう）

まず、電荷と電流の関係式は、

である。電流を から になるまでに流れた電荷を 、時刻を から とすると、その間に電荷が失う静電気力による位置エネルギー（電流がする仕事）は、電位の定義より、

と求められる（途中で → → へと置換積分した）。