ブリッジ回路
概要
抵抗値がわからないものがあるときに、検流計を組み込んだブリッジ回路という回路を組むことによって、精密にその抵抗値を測定することができる。
ここでは、高校物理でよく登場する 「ホイートストンブリッジ回路」の原理と公式を学ぼう。他にも、棒状の抵抗の途中に検出計を刺す「メートル回路」などがあるが、やっていることは同じ。(気になる方は長旅Pさんの動画がおすすめ)
結論から言うと、
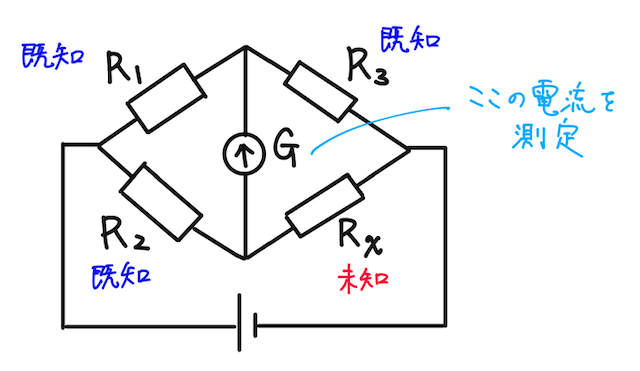
- 電流を精密に測定できる検流計
- 抵抗値がわかっている抵抗器(抵抗値を
とする) - 抵抗値がわからない抵抗器(抵抗値を
とする)
を組み合わせて、下のような回路を組んで、検流計に流れる電流を測定する。
が成り立つ(これを平衡条件と呼んだりする)。この式により、知りたかった抵抗値
とバシッと求めることができる。
平衡条件のイメージ
まずは、
検流計に電流が流れないということは、下の図で点Bと点Cの電位差がないということを意味する。
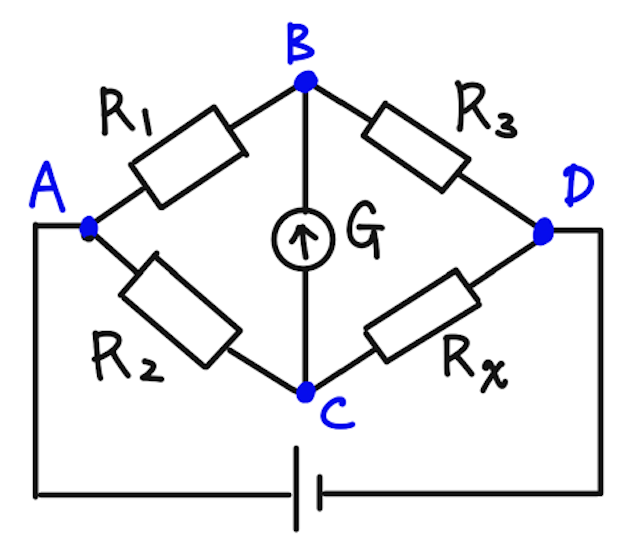
よって、点Aと点Dの電位差を考えたときに、A→BとB→Dの電位差の比と、A→CとC→Dの電位差の比が等しくなる。
さて、検流計に電流が流れないので、A→BとB→Dには同じ電流が流れる。このときオームの法則から、A→BとB→Dの電位差の比は、抵抗値
同様に、A→CとC→Dの電位差の比は、抵抗値
よってこれらの比が等しいので、
が成立する。
この「比で捉えるイメージ」はとてもとても大事。
式で考える
回路が複雑になってもいいように、一から立式をして求めることもやってみよう。
下のように電流を設定する。
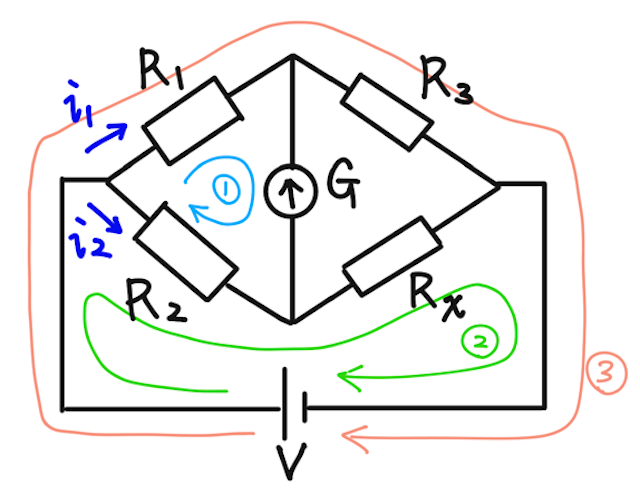
(検流計には電流が流れないので、
- 未知数:
の3つ - 立式:ループ①〜③でキルヒホッフの第二法則で3つ
となるので解けそうだ。(なるべく計算が楽になるように、つまり式の中の未知数が少なくなるようにループを設定するのが大事)
実際にキルヒホッフの第二法則で立式をすると、
ループ①
(オームの法則を用いている)
ループ②
(
ループ③
これらを解いていくと、
これらを
と確かに求められる。
補足
検流計に電流が流れなくなるので、検流計の内部抵抗の影響を考えなくて良いのが、ブリッジ回路で抵抗値を測定するメリットの一つ。
また、パッと見は違うけれども、下のような回路もホイートストンブリッジになっている。
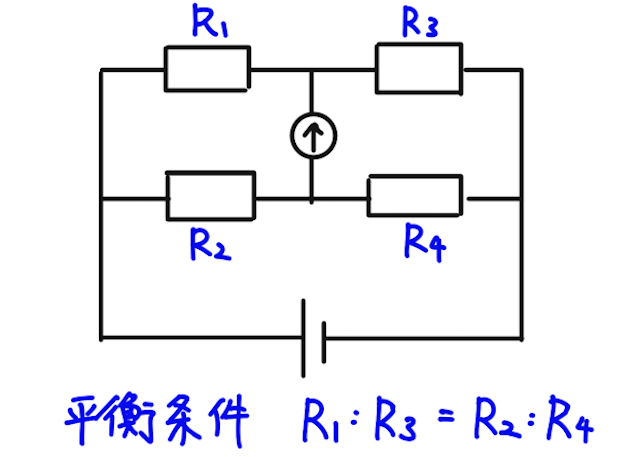
関連動画






