マイヤーの関係式

概要

定圧モル比熱 と 定積モル比熱 の間には、次の関係式が成り立つ。これをマイヤーの関係式という。本によってはメイヤーの関係式とも書かれている。

単原子分子の理想気体であれば、

であるので、マイヤーの関係式は当然成り立つわけだが、この関係式がすごいのは、単原子分子でなくても成り立つというところ。

導出

定圧モル比熱 の辞書で行った、単原子分子の場合での証明を少し応用すれば示すことができる。

の理想気体を定圧変化させて、温度が だけ上がったとする。ここでの熱力学第一法則の式を考えよう。（単原子分子とは限らないので、内部エネルギーの の表現は使えないことに注意！）

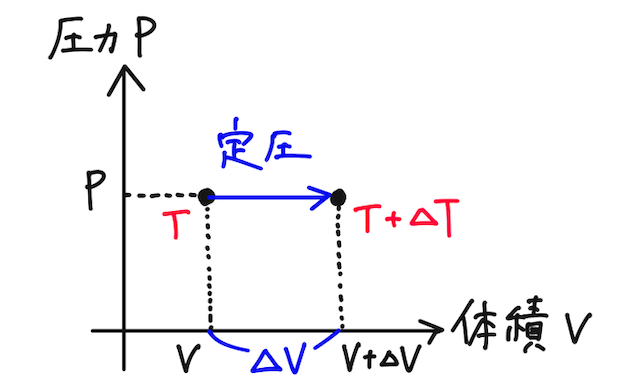
①この変化で受け取った熱量は、モル比熱の定義から、

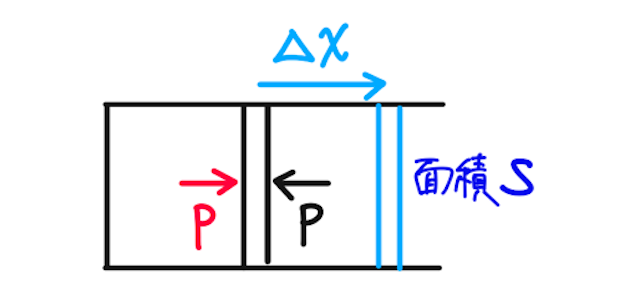
②さらに、外部にした仕事を考えると（この変化では、体積が増えているので、気体が正の仕事をする）、

※理解できない方は、面積 のピストンを だけ押していると考えよう。そうすると、外部にした仕事は、

と求められる。

ここで、状態方程式より、変化前と変化後の状態において、

が成り立つので、辺々引いて、

を得る。よって、気体がこの定圧変化により外部にした仕事は、

となる。

③そして最後に、内部エネルギーの変化は、定積モル比熱 を使えば、

と表せる（これは単原子分子でなくても成り立つのであった、詳しくは定積モル比熱の辞書を確認）。よって、熱力学第一法則より、

となって、マイヤーの関係式が導かれた。

補足

そんなに主役級に使うことはないが、ポアソンの法則の導出で使ったり、問題集の解説に書いてあったりするので、頭の片隅にちょこんと置いておくと良い。