同じものを含む順列

概要

同じものが 個、 個、 個ずつ、全部で 個あるとき、全てを並べる順列の総数は、

通りとなる。（ただし、）

ここでは3種類で考えているが、何種類でも使える。 下の例を確認しよう。

これは、覚えるよりもイメージを持っておくことで、応用問題にも対応できるようになるので、下の解説まで確認しよう。

例

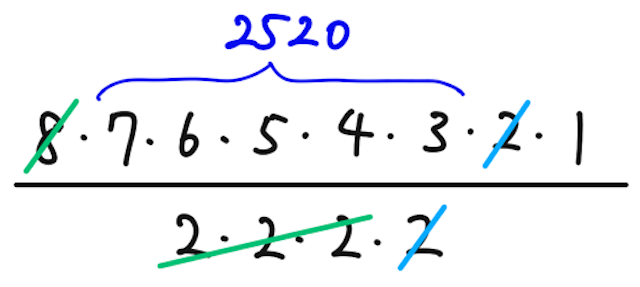
【問1】アルファベット A, A, B, B, C が書かれた5枚のカードがある。これらを並べる総数を求めよ。

【答1】

と求められる。

【問2】アルファベット A, A, B, B, C, C, D, D が書かれた8枚のカードがある。これらを並べる総数を求めよ。

【答2】

と求められる。 を計算するのはめんどくさいので、書き下して約分していこう。

解説

なんで で割らないといけないんだ！びっくりマーク付きすぎじゃね？という方もいると思うので、下のイメージを持っておくようにしよう。

例えば、上の例1で考えよう。

アルファベット A, A, B, B, C が書かれた5枚のカードを並べるとき、例えば一つの並べ方として、

• A, A, B, B, C ①

がある。これで1通り。

ここで、

• 2枚のAが、異なるカードA1, A2に
• 2枚のAが、異なるカードB1, B2に

変わったとすると、

• A1, A2の並べ方が 通り
• B1, B2の並べ方が 通り

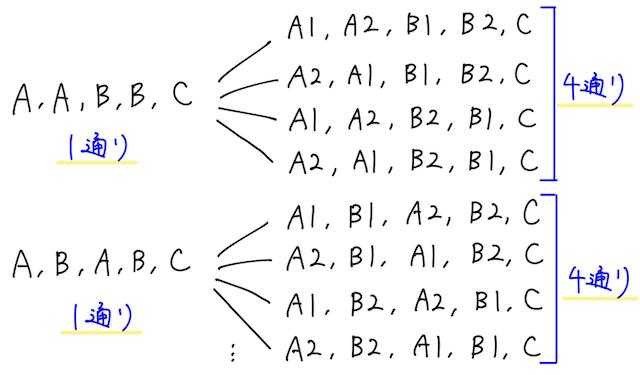
あるので、①の1つの並べ方から、

• A1, A2, B1, B2, C
• A2, A1, B1, B2, C
• A1, A2, B2, B1, C
• A2, A1, B2, B1, C

と、並べ方が4通りに増える。この4通りというのは、つまり、A1, A2の並べ方、B1, B2の並べ方を掛けた、

で求められる。そして、この4通りというのは、A, A, B, B, Cが特別だったからではなく、他の並べ方でも同様に4通りずつに増える。

そこで、A1, A2, B1, B2, Cの5枚のカードを並べるとすると、この場合は全てのカードが違うので、誰もが知っている通り、並べ方は

となる。

よって、元のA, A, B, B, Cの5枚のカードの並べ方は、

と求められる。

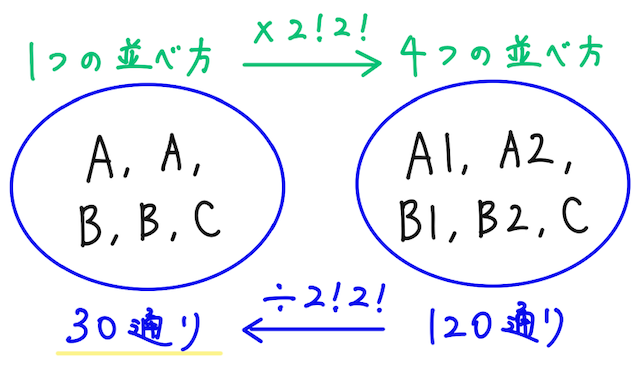
つまり、同じカードをもし違うカードと見たときに、1つの並べ方が何通りに増えるかを考えて、全て違うカードだった場合の並べ方の総数を、その重複する数で割って求めている。 このイメージを大事にしよう！