極座標系の運動方程式

概要

質量 の物体が力 を受けて運動するような2次元での運動を考えるとき、運動方程式の立て方としては、普通は 軸と 軸を設定して、

と式を立てる。これにより加速度がわかり、積分していくことで、時間の関数として位置を把握することができる。

これについて少し深く考えてみると、 軸と 軸というのは直交座標として定めていることがわかる。

では目線を変えて、同じ物体の運動を、極座標で眺めるとどのように運動方程式が記述できるのだろうか。（極座標というのは、原点 からの距離 と、 軸正の向きからの角度 で座標を表す方法であり、まだ学んでない方はこちらから動画で学んでおこう）

なんでこんなものを考えるのかというと、中心力を受けて運動するような場合には となるので、極座標で運動方程式を考えた方が処理しやすいことがあるため。これにより例えば、ややこしい円運動や楕円軌道の運動の式が考えやすくなる。（現実世界で起こっている、物体の運動そのものは変わらず、それをどのように座標を置いて考察していくかだけの違いなので、頭を混乱させないように気をつけよう）

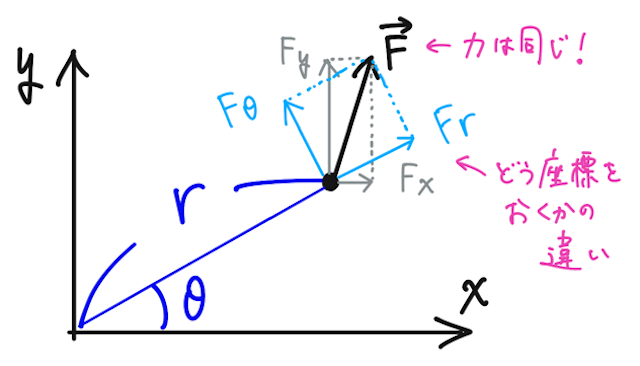
結論としては、極座標の運動方程式は次のようになる。

動径方向（ 方向）：

動径に垂直な方向（ 方向）：

ただし、 は、それぞれ力の動径方向の成分（ が増加する方向が正）、力の動径に垂直な方向（ が増加する方向が正）の成分を表す。

また、ドットは見たことない方も多いと思うが、画面の汚れやこぼれ落ちた鼻くそではなく、時間微分を表す。2つ付いていたら時間での2階微分。

証明については、割と長くなるので、是非動画で確認してみよう。

• 受験メモ山本さんの動画（後半に証明）
• ヨビノリさんの動画（ベクトルのまま証明されていて発展的）
• 東大物理学科卒ひぐまさんの動画（復習にも最適）

がおすすめ。

等速円運動との関係

ではみんな大好き等速円運動で、極座標系での運動方程式を考えてみよう。

等速円運動では、半径が一定なので、

また、角速度も一定なので、

となるので、動径方向と、動径に垂直な方向の運動方程式はそれぞれ、

となる。ここで、 は が増加する方向が正なので、 が向心力になること、 は角速度 であることを用いると、

となり、おなじみの式が出来上がる。

ちなみに、この極座標系での運動方程式から、 でありさえすれば、 の運動方程式は成り立つことがわかるので、等速でない円運動でも の運動方程式が使えることがわかる。（何気なく使っているかもしれないが、このような背景がある）

補足

動径に垂直な方向の運動方程式：

を変形すると、とある保存則が登場する。商の微分と合成関数の微分から、

と変形できることがわかるので、ここで の運動を考えると、

であることが示される。（ は時間によらない定数という意味）

これを変形すれば、

となり、面積速度一定の法則を示していることがわかる（ケプラーの第二法則で登場したもの）。つまり、中心力のみを受けて運動する物体は、面積速度一定の法則が成り立つことを意味する。