熱効率
概要
気体の状態を変化させ、一巡して元の状態の戻すことを考える。下の状態に戻すということは、温度も元に戻るので、内部エネルギーも元通りになる。
この一巡の間に、気体が受け取る(吸収する)熱量の総和を
そうすると、熱力学第一法則から、
となるので、変形すると
これを日本語にすると、気体が正味受け取った熱量(受け取った熱量 − 捨てた熱量)は、気体が正味外部にする仕事(外部にする仕事 − 外部からされる仕事)に等しい、ということ。
これを活かして、受け取った熱量を、外部にする仕事に変える機関を熱機関という。自動車のエンジンやエアコンなどはこの原理を用いている。物理に感謝したくなるタイミングの1つ。
そして、熱期間がどれくらい効率の良いものなのかを測る指標が熱効率で、次のように定義される。
つまり、受け取った熱量の総和(
この熱効率が大きければ、受け取った熱量を効率よく仕事に使える事になる。
しかし実は、熱効率は
となるが、気体が一巡する間に捨てる熱量の総和(
熱効率を求める際は、求めやすい式で求めればOK。
例
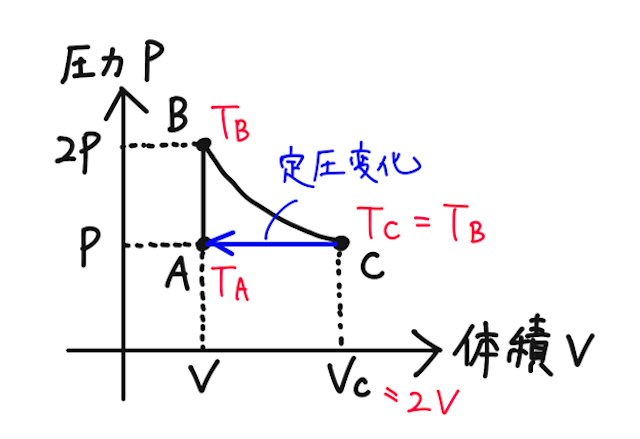
【問】単原子分子の理想気体の状態を、下の図のように
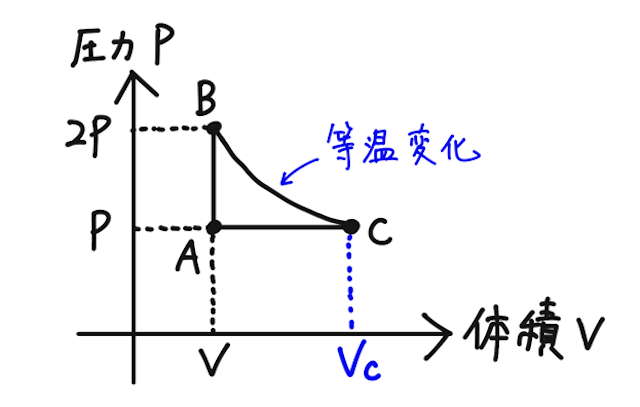
【答】それぞれの経路での、気体が外部からされた仕事、気体が受け取った熱を求めていく。直接求めにくいものは、熱力学第一法則で求まることが多い。
途中で、熱を受け取っているのか、捨てているのかわかりづらい経路があるので、方向が明確にわからないものがもしあれば、ここでは気体が外部からされた仕事や受け取った熱を正として考えることにする。
ややこしいがとても大事で頻出テーマなので、下のまとめ表を見ながら頭を整理しよう!
■
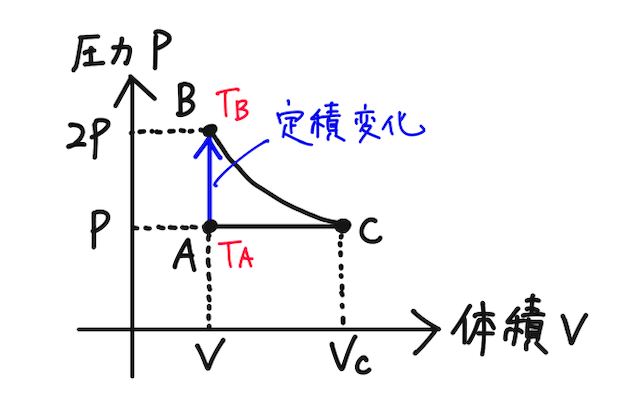
定積変化なので、気体が外部からされた仕事は
受け取った熱量は、直接求められないので、熱力学第一法則を用いる。そのためにまずは内部エネルギーを考える。状態
で求められる。次に、状態
となる。下から上を引くと、
となるので、内部エネルギーの変化は
と求まる。よって、
となる。
■
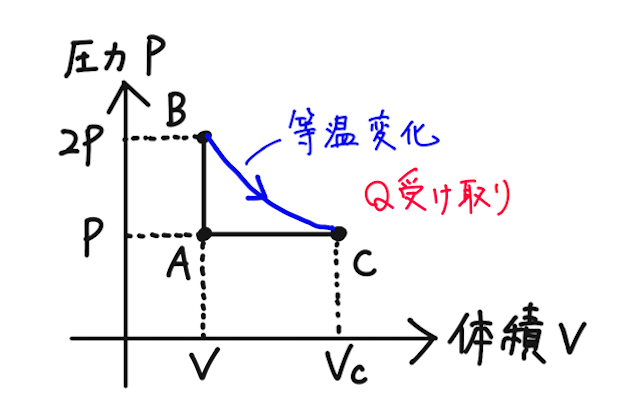
問題文から、受け取った熱量は
気体が外部にした仕事を求めよう。
等温変化なので、内部エネルギーは変化しない。よって、外部にした仕事を
となり、確かに気体は外部に対して正の仕事をしている。(このように、仕事の方向がはっきりわかっている時は、そっちを正として文字を置いてしまってOK。「後でこんがらがるわ!」という方は、最初に決めた正の向きに、忠実に文字を置いて考えよう)
■
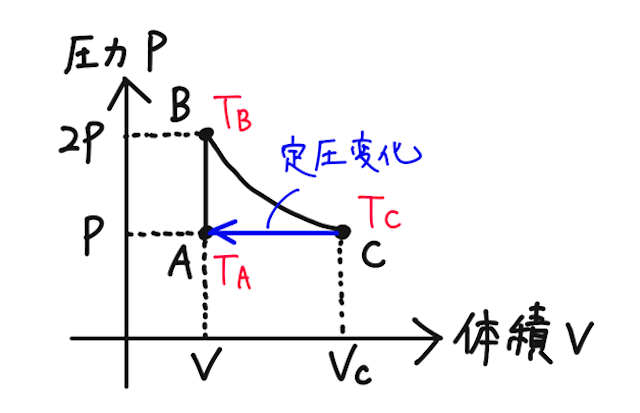
定圧変化であり、気体が外部からされた仕事は、
となるので、
これと、上で考えた状態
を比較すれば
が得られる。よって気体が外部からされた仕事は、
と求められる。
では、受け取った熱量を
状態
で求められる。
※上で議論した通り、等温変化より
気体の物質量を
これらを代入して、
と求められる。
よって熱力学第一法則より
となり、熱を捨てていることがわかる。(受け取った熱量を
■ 熱効率の計算
よって、経路中の熱の出し入れや気体の仕事を全てをまとめると、
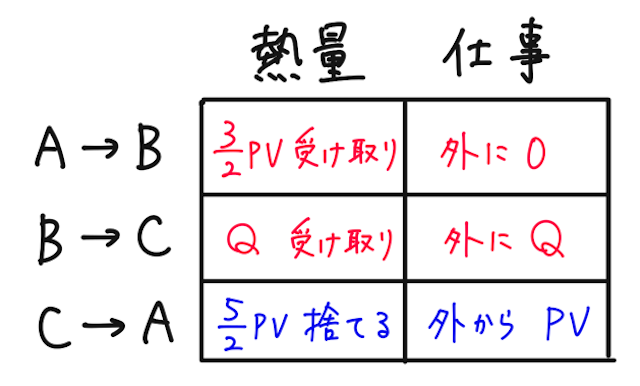
となるので、熱効率は、
と求められる。
で求めてももちろんOK。
関連動画








