概要
関数 で、 に対して がただ一つに決まるとき、 は の関数となり、 と書く。この を の逆関数という。
理解できない日本語なので、基礎となる知識から整理しよう。解ければいい派の人は、下の例題で確認しよう。
まず、「 は の関数」の定義で大事なことは、定義域()から値を一つとってくると、値域()の中の値がただ一つ決まるということ(なので、例えばまん丸な円の方程式は関数とは言えない)。このとき、 逆に考えて、 「値域()の中の値を一つとってきたときに、定義域()の中の値が常にただ一つに決まるだろうか? 」 ということを考えてみる。
実はこれはいつも成り立つわけでは無い。
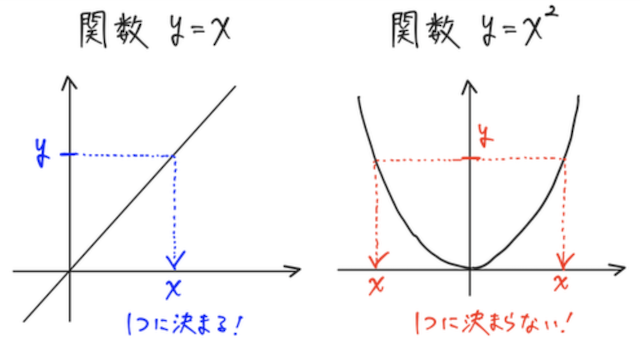
(※定義域・値域をとっくに忘れた方は、定義域はこちらの辞書、値域はこちらの辞書から確認しよう。)
上のグラフの例だと は、値域()の中の値を一つとってきたときに、定義域()の中の値がただ一つに決まるが、 は決まらない。
のように、もしこれがただ一つに決まるのであれば、関数の定義から、 「 は の関数」 とみることができる(この関数では、 が定義域で、 が値域となる)。それを元の関数 の 「逆関数」と呼び、 と書く 。つまり、
が成り立つ。花火では無いが、関数 、下から見るか、横から見るか、という話。
ちなみに、 は 「エフインバース」 と呼ぶことが多い。プロレス技の名前みたいでカッコいいので、是非これも呼べるようになろう。
「逆関数を求めよ」というときは、逆関数の定義域を で、値域を とすることが多い(「逆関数 を求めよ」など)ので、 の と を入れ替えて答えればOK。このときに、元の関数 の値域が、逆関数 の定義域になる。この対応がややこしいので、頭を整理しよう。

例
【問】 の逆関数 を求めよ。
【答】関数 を について解くと、
よって、 と を入れ替えて、逆関数 は
と求められる。
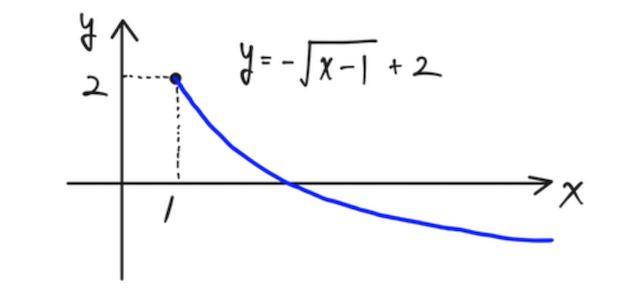
ちなみに、 のグラフは以下のようになり、 を一つとってきたときに、 の値がただ一つに決まるのがわかるので、逆関数が存在する。
補足
逆関数 は、元の関数の と を入れ替えてるので、 つのグラフを書くと に関して対称になる。








